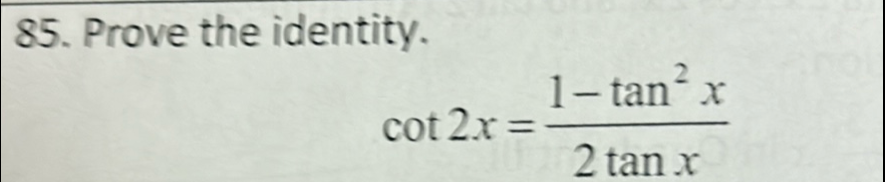AI tutor
Full solution
Q. . Prove the identity.
- Express : We start by expressing in terms of sine and cosine functions using the identity .
- Use double angle formulas: Now we use the double angle formulas for sine and cosine to express and in terms of and . and
- Substitute formulas into : Substitute the double angle formulas into the expression for .
- Express and : We know that , so we can express and in terms of . and
- Factor out : Substitute and in terms of into the expression for .
- Cancel out terms: Factor out from the numerator.
- Arrive at desired identity: Cancel out the terms in the numerator and denominator.
- Arrive at desired identity: Cancel out the terms in the numerator and denominator.We have arrived at the identity we were asked to prove.
More problems from Composition of linear and quadratic functions: find a value
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help