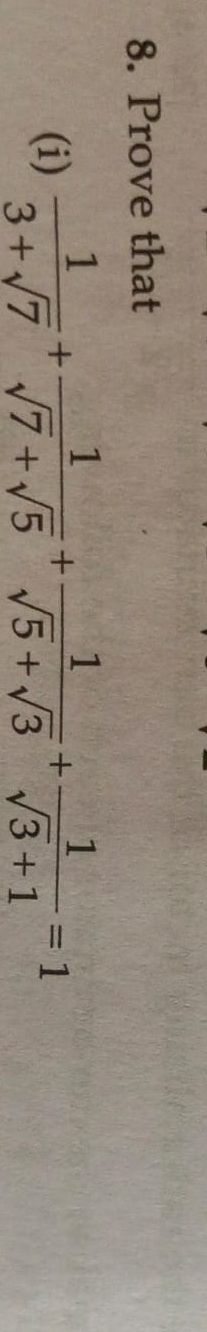Prove that (i) (1)/(3+sqrt7)+(1)/(sqrt7+sqrt5)+(1)/(sqrt5+sqrt3)+(1)/(sqrt3+1)=1

Question

Prove that (i)  (1)/(3+sqrt7)+(1)/(sqrt7+sqrt5)+(1)/(sqrt5+sqrt3)+(1)/(sqrt3+1)=1

Bytelearn · Accepted Answer

Rationalize Denominators: Rationalize the denominator of each fraction. Rationalizing the denominator of the first fraction: $$ \frac{1}{3+\sqrt{7}} \cdot \frac{3-\sqrt{7}}{3-\sqrt{7}} = \frac{3-\sqrt{7}}{(3+\sqrt{7})(3-\sqrt{7})} $$ Rationalizing the denominator of the second fraction: $$ \frac{1}{\sqrt{7}+\sqrt{5}} \cdot \frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}-\sqrt{5}} = \frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})} $$ Rationalizing the denominator of the third fraction: $$ \frac{1}{\sqrt{5}+\sqrt{3}} \cdot \frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}-\sqrt{3}} = \frac{\sqrt{5}-\sqrt{3}}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})} $$ Rationalizing the denominator of the fourth fraction: $$ \frac{1}{\sqrt{3}+1} \cdot \frac{\sqrt{3}-1}{\sqrt{3}-1} = \frac{\sqrt{3}-1}{(\sqrt{3}+1)(\sqrt{3}-1)} $$Simplify Denominators: Simplify the denominators using the difference of squares formula. Simplify the denominator of the first fraction: $$ \frac{3-\sqrt{7}}{3^2-(\sqrt{7})^2} = \frac{3-\sqrt{7}}{9-7} = \frac{3-\sqrt{7}}{2} $$ Simplify the denominator of the second fraction: $$ \frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7})^2-(\sqrt{5})^2} = \frac{\sqrt{7}-\sqrt{5}}{7-5} = \frac{\sqrt{7}-\sqrt{5}}{2} $$ Simplify the denominator of the third fraction: $$ \frac{\sqrt{5}-\sqrt{3}}{(\sqrt{5})^2-(\sqrt{3})^2} = \frac{\sqrt{5}-\sqrt{3}}{5-3} = \frac{\sqrt{5}-\sqrt{3}}{2} $$ Simplify the denominator of the fourth fraction: $$ \frac{\sqrt{3}-1}{(\sqrt{3})^2-1^2} = \frac{\sqrt{3}-1}{3-1} = \frac{\sqrt{3}-1}{2} $$Add Simplified Fractions: Add the simplified fractions together. $$ \frac{3-\sqrt{7}}{2} + \frac{\sqrt{7}-\sqrt{5}}{2} + \frac{\sqrt{5}-\sqrt{3}}{2} + \frac{\sqrt{3}-1}{2} $$ Since all denominators are the same, we can combine the numerators: $$ \frac{(3-\sqrt{7}) + (\sqrt{7}-\sqrt{5}) + (\sqrt{5}-\sqrt{3}) + (\sqrt{3}-1)}{2} $$Cancel Terms in Numerator: Simplify the numerator by canceling out the terms. $$ \frac{3 - \cancel{\sqrt{7}} + \cancel{\sqrt{7}} - \cancel{\sqrt{5}} + \cancel{\sqrt{5}} - \cancel{\sqrt{3}} + \cancel{\sqrt{3}} - 1}{2} $$ The terms with square roots cancel each other out, leaving us with: $$ \frac{3 - 1}{2} = \frac{2}{2} $$Final Fraction: Simplify the final fraction. $$ \frac{2}{2} = 1 $$

$8$ . Prove that $\newline$ (i) $\frac{1}{3+\sqrt{7}}+\frac{1}{\sqrt{7}+\sqrt{5}}+\frac{1}{\sqrt{5}+\sqrt{3}}+\frac{1}{\sqrt{3}+1}=1$

Full solution

More problems from Solve quadratic inequalities

Related topics

888. Prove that\newline(i) 13+7+17+5+15+3+13+1=1 \frac{1}{3+\sqrt{7}}+\frac{1}{\sqrt{7}+\sqrt{5}}+\frac{1}{\sqrt{5}+\sqrt{3}}+\frac{1}{\sqrt{3}+1}=1 3+7​1​+7​+5​1​+5​+3​1​+3​+11​=1

$8$ . Prove that $\newline$ (i) $\frac{1}{3+\sqrt{7}}+\frac{1}{\sqrt{7}+\sqrt{5}}+\frac{1}{\sqrt{5}+\sqrt{3}}+\frac{1}{\sqrt{3}+1}=1$