Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

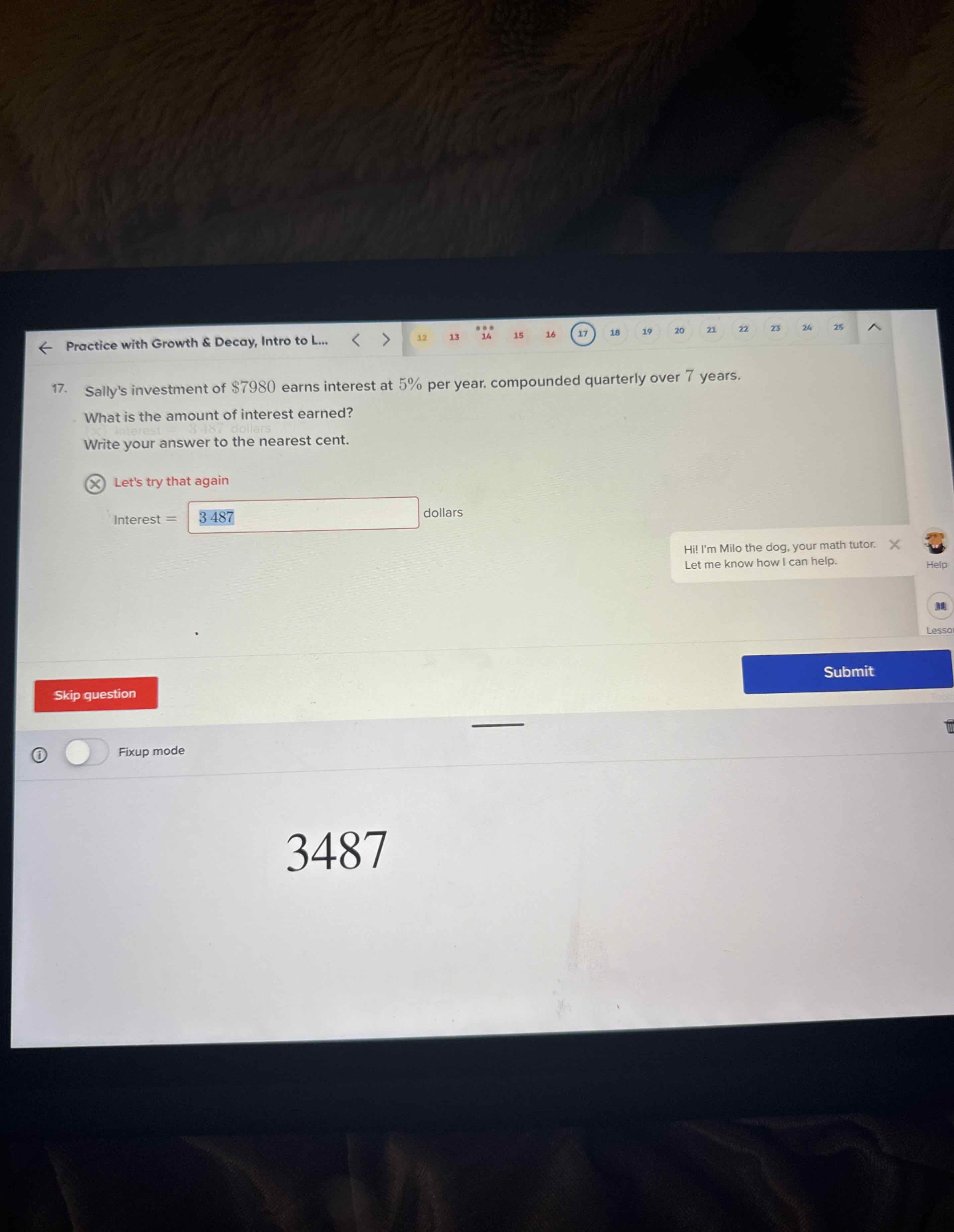
Sally's investment of $7980 earns interest at 5% per year. compounded quarterly over 7 years. What is the amount of interest earned? Write your answer to the nearest cent.

Sally's investment of $7980\$7980 earns interest at 5%5\% per year. compounded quarterly over 77 years.\newline What is the amount of interest earned? \newlineWrite your answer to the nearest cent.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find probabilities using the binomial distributionright chevron icon

Full solution

Q. Sally's investment of $7980\$7980 earns interest at 5%5\% per year. compounded quarterly over 77 years.\newline What is the amount of interest earned? \newlineWrite your answer to the nearest cent.
  1. Identify Formula: Identify the formula for compound interest.\newlineCompound Interest Formula: A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}\newlineWhere:\newlinePP = principal amount ($\$\(7980\))\(\newline\)\(r\) = annual interest rate (\(5\%\) or \(0.05\))\(\newline\)\(n\) = number of times interest applied per time period (\(4\), since quarterly)\(\newline\)\(t\) = time the money is invested for in years (\(7\))
  2. Plug Values: Plug the values into the formula to calculate the final amount.\(\newline\)\(A = 7980(1 + 0.05/4)^{4\times7}\)\(\newline\)\(A = 7980(1 + 0.0125)^{28}\)\(\newline\)\(A = 7980(1.0125)^{28}\)
  3. Calculate Power: Calculate the power \((1.0125)^{28}\).\((1.0125)^{28} \approx 1.4116\)
  4. Multiply Principal: Multiply the principal amount by the result from Step \(3\).\(\newline\)\(A = 7980 \times 1.4116\)\(\newline\)\(A \approx 11268.57\)
  5. Calculate Interest: Calculate the interest earned by subtracting the principal from the final amount.\(\newline\)\(\text{Interest} = \text{Final Amount} - \text{Principal}\)\(\newline\)\(\text{Interest} = 11268.57 - 7980\)\(\newline\)\(\text{Interest} \approx 3288.57\)

More problems from Find probabilities using the binomial distribution

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 9 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 9 months ago

Question
Y Y is the number of desserts available in a randomly chosen restaurant.\newlineIs the random variable Y Y discrete or continuous?\newlineChoices:\newline[A]discrete \text{[A]discrete} \newline[B]continuous \text{[B]continuous}
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous for all real numbers?\newlineg(x)=ln⁡(x) g(x)=\ln (x) \newlinef(x)=1x f(x)=\frac{1}{x} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newlineD Neither g g nor f f
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous at x=−1 x=-1 ?\newlineg(x)=sin⁡(x+1) g(x)=\sin (x+1) \newlinef(x)=1x−1 f(x)=\frac{1}{x-1} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newline(D) Neither g g nor f f
Get tutor helpright-arrow

Posted 8 months ago

Question
Let g g be a continuous function on the closed interval [−1,4] [-1,4] , where g(−1)=−4 g(-1)=-4 and g(4)=1 g(4)=1 .\newlineWhich of the following is guaranteed by the Intermediate Value Theorem?\newlineChoose 11 answer:\newline(A) g(c)=−3 g(c)=-3 for at least one c c between −1-1 and 44\newline(B) g(c)=3 g(c)=3 for at least one c c between −4-4 and 11\newline(C) g(c)=−3 g(c)=-3 for at least one c c between −4-4 and 11\newline(D) g(c)=3 g(c)=3 for at least one c c between −1-1 and 44
Get tutor helpright-arrow

Posted 8 months ago

View all (89)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant