Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

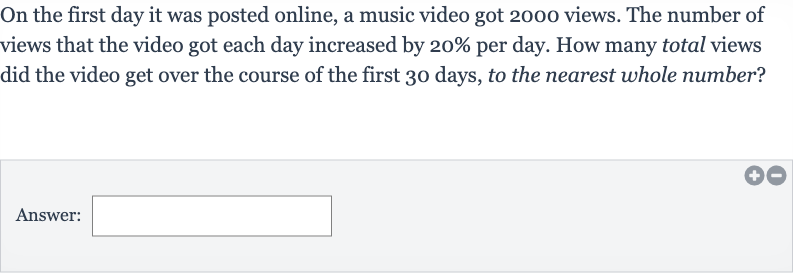
On the first day it was posted online, a music video got 2000 views. The number of views that the video got each day increased by 20% per day. How many total views did the video get over the course of the first 30 days, to the nearest whole number? Answer:

On the first day it was posted online, a music video got 20002000 views. The number of views that the video got each day increased by 20% 20 \% per day. How many total views did the video get over the course of the first 3030 days, to the nearest whole number?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Exponential growth and decay: word problemsright chevron icon

Full solution

Q. On the first day it was posted online, a music video got 20002000 views. The number of views that the video got each day increased by 20% 20 \% per day. How many total views did the video get over the course of the first 3030 days, to the nearest whole number?\newlineAnswer:
  1. Identify initial number of views: Identify the initial number of views and the daily increase rate.\newlineThe initial number of views V0V_0 is 20002000, and the daily increase rate rr is 20%20\% or 0.200.20 in decimal form.
  2. Determine formula for total views: Determine the formula for the total number of views after a certain number of days.\newlineThe total number of views VV after nn days can be calculated using the formula for the sum of a geometric series: V=V0×[1−rn1−r]V = V_0 \times \left[\frac{1 - r^n}{1 - r}\right], where rr is the common ratio (1+daily increase rate)(1 + \text{daily increase rate}).
  3. Calculate common ratio: Calculate the common ratio for the geometric series.\newlineThe common ratio rr is 1+1 + the daily increase rate, which is 1+0.20=1.201 + 0.20 = 1.20.
  4. Calculate total views after 3030 days: Calculate the total number of views after 3030 days using the formula.\newlineSubstitute the values into the formula: V=2000×[(1−1.2030)(1−1.20)]V = 2000 \times \left[\frac{(1 - 1.20^{30})}{(1 - 1.20)}\right].
  5. Evaluate expression within brackets: Evaluate the expression within the brackets first.\newlineCalculate 1.20301.20^{30} and then subtract it from 11.
  6. Calculate denominator of fraction: Calculate the denominator of the fraction.\newlineThe denominator is 1−1.201 - 1.20, which is −0.20-0.20.
  7. Divide result by denominator: Divide the result from Step 55 by the result from Step 66. This will give us the total multiplier to be applied to the initial number of views.
  8. Multiply initial views by total multiplier: Multiply the initial number of views by the total multiplier to find the total number of views. This will give us the total number of views the video got over the course of the first 3030 days.
  9. Round result to nearest whole number: Round the result to the nearest whole number as the final answer.
  10. Perform calculations: Perform the calculations.\newlineFirst, calculate 1.20301.20^{30}: \newline1.2030≈237.376311.20^{30} \approx 237.37631\newlineThen, subtract this from 11: \newline1−237.37631≈−236.376311 - 237.37631 \approx -236.37631\newlineNow, divide by −0.20-0.20: \newline−236.37631/−0.20≈1181.88155-236.37631 / -0.20 \approx 1181.88155\newlineFinally, multiply by the initial number of views: \newline1181.88155×2000≈2363763.11181.88155 \times 2000 \approx 2363763.1\newlineRound to the nearest whole number: \newline2363763.1≈23637632363763.1 \approx 2363763

More problems from Exponential growth and decay: word problems

Question
Use the following function rule to find f(2) f(2) .\newlinef(x)=11⋅(9)x+8 f(x) = 11 \cdot (9)^x + 8 \newlinef(2)= f(2) = _____
Get tutor helpright-arrow

Posted 5 months ago

Question
Raymond works for a pharmaceutical company that is testing the effectiveness of a new medication. He gave one of the study participants 400400 milligrams of the medication, and he knows the amount remaining in the participant's body will decrease by a factor of 1/31/3 each hour.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the amount of medication, yy, remaining in the participant's body after xx hours.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
A colony of 100100 bacteria doubles in size every 6060 hours. What will the population be 180180 hours from now??
Get tutor helpright-arrow

Posted 4 months ago

Question
Charlotte opened a savings account and deposited $800.00\$800.00 as principal. The account earns 8%8\% interest, compounded annually. What is the balance after 1010 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.
Get tutor helpright-arrow

Posted 4 months ago

Question
Bob rented a car for a flat fee of `$150` and an additional `$10` per day. Write a linear function that represents the total cost, f(x)f(x), after xx days.
Get tutor helpright-arrow

Posted 10 months ago

Question
Sally purchased a laptop for `$800` and has to pay a service fee of `$20` for each day until it is delivered. Write a linear function to represent the total cost, h(x)h(x), after xx days.
Get tutor helpright-arrow

Posted 10 months ago

Question
Kevin invested $1,000\$1,000 in a savings account with a daily interest rate of 0.1%0.1\%. Write an exponential function to represent the total amount, s(x)s(x), in his account after xx days.
Get tutor helpright-arrow

Posted 9 months ago

Question
A=2450+740s A=2450+740 s \newlineThe total amount, A A , in thousands of dollars, of scholarship money given out by a college throughout its history at a time of s s semesters after the summer of the year 20002000 is given by the equation. What was the total amount of scholarship money, in thousands of dollars, given out by the college up to the summer of the year 20002000 ?
Get tutor helpright-arrow

Posted 5 months ago

Question
T=235+980d T=235+980 d \newlineThe torque, T T , in newton-meters, on a diving board with a 100100 kilogram weight placed d d meters from the diving board's fulcrum is given by the equation. How much torque in newton-meters is on the diving board when the weight is placed at the fulcrum?
Get tutor helpright-arrow

Posted 8 months ago

Question
R=42−0.7t R=42-0.7 t \newlineQuinn returned home one summer's day to find it extremely hot. He turned the air conditioner on, and the room's temperature began decreasing at a constant rate. The given equation shown gives the room's temperature, R R , in degrees Celsius, t t minutes after Quinn turned on the air conditioner. What was the room's temperature, in degrees Celsius, when Quinn returned home?
Get tutor helpright-arrow

Posted 7 months ago

View all (161)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant