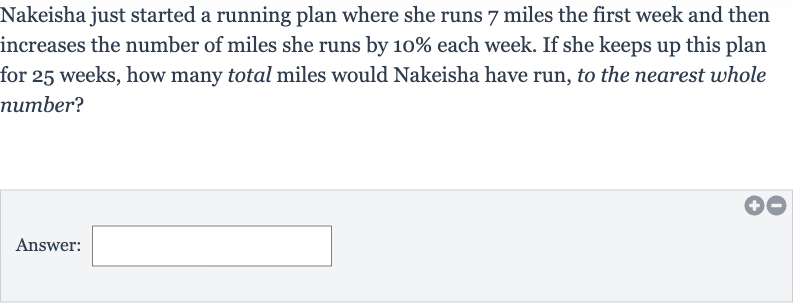
Nakeisha just started a running plan where she runs 7 miles the first week and then increases the number of miles she runs by 10% each week. If she keeps up this plan for 25 weeks, how many total miles would Nakeisha have run, to the nearest whole number? Answer:

Question

Nakeisha just started a running plan where she runs 7 miles the first week and then increases the number of miles she runs by  10% each week. If she keeps up this plan for 25 weeks, how many total miles would Nakeisha have run, to the nearest whole number? Answer:

Bytelearn · Accepted Answer

Identify initial amount and rate: Identify the initial amount of miles and the rate of increase. Nakeisha starts with 7 miles in the first week and increases her running distance by 10% each week. Initial miles (a) = 7 Rate of increase (r) = 10% or 0.10Calculate total miles per week: Calculate the total miles run for each week. The total miles run in each subsequent week can be calculated using the formula for the nth term of a geometric sequence: Week n miles = a * (1 + r)^(n-1) We will use this formula to calculate the miles run each week and then sum them up for 25 weeks.Calculate total miles over 25 weeks: Calculate the total miles run over 25 weeks. We need to sum up the miles for each week from week 1 to week 25. Total miles = a + a*(1+r) + a*(1+r)^2 + ... + a*(1+r)^(25-1) This is the sum of a finite geometric series.Use formula for sum of series: Use the formula for the sum of a finite geometric series. The sum S of the first n terms of a geometric series is given by: S = a * (1 - (1 + r)^n) / (1 - (1 + r)) We will substitute n = 25, a = 7, and r = 0.10 into this formula to find the total miles.Perform calculation using formula: Perform the calculation using the formula. S = 7 * (1 - (1 + 0.10)^25) / (1 - (1 + 0.10)) S = 7 * (1 - (1.10)^25) / (1 - 1.10) S = 7 * (1 - (1.10)^25) / (-0.10)Calculate exact total and round: Calculate the exact total and then round to the nearest whole number. First, calculate (1.10)^25, then substitute it back into the formula to find S. After finding S, round it to the nearest whole number.Use calculator to find total: Use a calculator to find (1.10)^25 and then find S. (1.10)^25 ≈ 10.834705... S ≈ 7 * (1 - 10.834705...) / (-0.10) S ≈ 7 * (-9.834705...) / (-0.10) S ≈ 7 * 98.34705... S ≈ 688.42935... Rounded to the nearest whole number, S ≈ 688 miles.

Nakeisha just started a running plan where she runs $7$ miles the first week and then increases the number of miles she runs by $10 \%$ each week. If she keeps up this plan for $25$ weeks, how many total miles would Nakeisha have run, to the nearest whole number? $\newline$ Answer:

Full solution

More problems from Exponential growth and decay: word problems

Related topics

Nakeisha just started a running plan where she runs 777 miles the first week and then increases the number of miles she runs by 10% 10 \% 10% each week. If she keeps up this plan for 252525 weeks, how many total miles would Nakeisha have run, to the nearest whole number?\newlineAnswer:

Nakeisha just started a running plan where she runs $7$ miles the first week and then increases the number of miles she runs by $10 \%$ each week. If she keeps up this plan for $25$ weeks, how many total miles would Nakeisha have run, to the nearest whole number? $\newline$ Answer: