Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

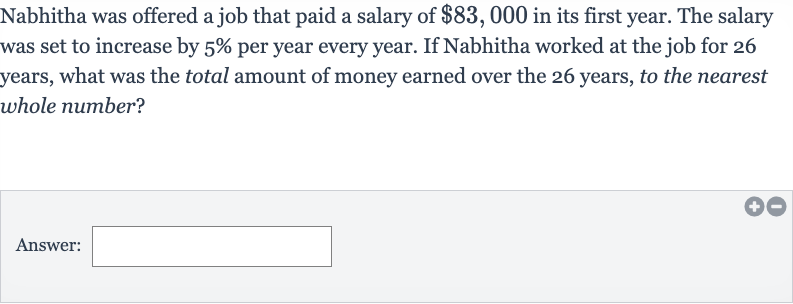
Nabhitha was offered a job that paid a salary of $83,000 in its first year. The salary was set to increase by 5% per year every year. If Nabhitha worked at the job for 26 years, what was the total amount of money earned over the 26 years, to the nearest whole number? Answer:

Nabhitha was offered a job that paid a salary of $83,000 \$ 83,000 in its first year. The salary was set to increase by 5% 5 \% per year every year. If Nabhitha worked at the job for 2626 years, what was the total amount of money earned over the 2626 years, to the nearest whole number?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Exponential growth and decay: word problemsright chevron icon

Full solution

Q. Nabhitha was offered a job that paid a salary of $83,000 \$ 83,000 in its first year. The salary was set to increase by 5% 5 \% per year every year. If Nabhitha worked at the job for 2626 years, what was the total amount of money earned over the 2626 years, to the nearest whole number?\newlineAnswer:
  1. Identify initial salary: Identify the initial salary and the annual increase percentage.\newlineNabhitha's initial salary is $83,000\$83,000, and it increases by 5%5\% each year.
  2. Determine formula for total salary: Determine the formula to calculate the total salary over 2626 years.\newlineThe salary increases exponentially, so we use the formula for the sum of a geometric series: Sn=a×(1−rn)/(1−r)S_n = a \times (1 - r^n) / (1 - r), where aa is the first term, rr is the common ratio, and nn is the number of terms.
  3. Calculate common ratio: Calculate the common ratio rr based on the annual increase.\newlineThe salary increases by 5%5\% each year, so the common ratio rr is 1+5100=1.051 + \frac{5}{100} = 1.05.
  4. Apply geometric series formula: Apply the formula for the sum of a geometric series to calculate the total salary.\newlineUsing the formula Sn=a×(1−rn)/(1−r)S_n = a \times (1 - r^n) / (1 - r), we substitute a=$83,000a = \$83,000, r=1.05r = 1.05, and n=26n = 26.\newlineS26=83,000×(1−1.0526)/(1−1.05)S_{26} = 83,000 \times (1 - 1.05^{26}) / (1 - 1.05)
  5. Calculate total salary: Calculate the total salary over 2626 years.\newlineS26=83,000×(1−1.0526)/(1−1.05)S_{26} = 83,000 \times (1 - 1.05^{26}) / (1 - 1.05)\newlineS26=83,000×(1−1.0526)/(−0.05)S_{26} = 83,000 \times (1 - 1.05^{26}) / (-0.05)\newlineS26=83,000×(1−4.291870)/(−0.05)S_{26} = 83,000 \times (1 - 4.291870) / (-0.05)\newlineS26=83,000×(−3.291870)/(−0.05)S_{26} = 83,000 \times (-3.291870) / (-0.05)\newlineS26=83,000×65.8374S_{26} = 83,000 \times 65.8374\newlineS26=5,464,442.2S_{26} = 5,464,442.2
  6. Round total salary: Round the total salary to the nearest whole number.\newlineThe total salary over 2626 years, rounded to the nearest whole number, is $5,464,442\$5,464,442.

More problems from Exponential growth and decay: word problems

Question
Use the following function rule to find f(2) f(2) .\newlinef(x)=11⋅(9)x+8 f(x) = 11 \cdot (9)^x + 8 \newlinef(2)= f(2) = _____
Get tutor helpright-arrow

Posted 5 months ago

Question
Raymond works for a pharmaceutical company that is testing the effectiveness of a new medication. He gave one of the study participants 400400 milligrams of the medication, and he knows the amount remaining in the participant's body will decrease by a factor of 1/31/3 each hour.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the amount of medication, yy, remaining in the participant's body after xx hours.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
A colony of 100100 bacteria doubles in size every 6060 hours. What will the population be 180180 hours from now??
Get tutor helpright-arrow

Posted 4 months ago

Question
Charlotte opened a savings account and deposited $800.00\$800.00 as principal. The account earns 8%8\% interest, compounded annually. What is the balance after 1010 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.
Get tutor helpright-arrow

Posted 4 months ago

Question
Bob rented a car for a flat fee of `$150` and an additional `$10` per day. Write a linear function that represents the total cost, f(x)f(x), after xx days.
Get tutor helpright-arrow

Posted 10 months ago

Question
Sally purchased a laptop for `$800` and has to pay a service fee of `$20` for each day until it is delivered. Write a linear function to represent the total cost, h(x)h(x), after xx days.
Get tutor helpright-arrow

Posted 10 months ago

Question
Kevin invested $1,000\$1,000 in a savings account with a daily interest rate of 0.1%0.1\%. Write an exponential function to represent the total amount, s(x)s(x), in his account after xx days.
Get tutor helpright-arrow

Posted 9 months ago

Question
A=2450+740s A=2450+740 s \newlineThe total amount, A A , in thousands of dollars, of scholarship money given out by a college throughout its history at a time of s s semesters after the summer of the year 20002000 is given by the equation. What was the total amount of scholarship money, in thousands of dollars, given out by the college up to the summer of the year 20002000 ?
Get tutor helpright-arrow

Posted 5 months ago

Question
T=235+980d T=235+980 d \newlineThe torque, T T , in newton-meters, on a diving board with a 100100 kilogram weight placed d d meters from the diving board's fulcrum is given by the equation. How much torque in newton-meters is on the diving board when the weight is placed at the fulcrum?
Get tutor helpright-arrow

Posted 8 months ago

Question
R=42−0.7t R=42-0.7 t \newlineQuinn returned home one summer's day to find it extremely hot. He turned the air conditioner on, and the room's temperature began decreasing at a constant rate. The given equation shown gives the room's temperature, R R , in degrees Celsius, t t minutes after Quinn turned on the air conditioner. What was the room's temperature, in degrees Celsius, when Quinn returned home?
Get tutor helpright-arrow

Posted 7 months ago

View all (161)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant