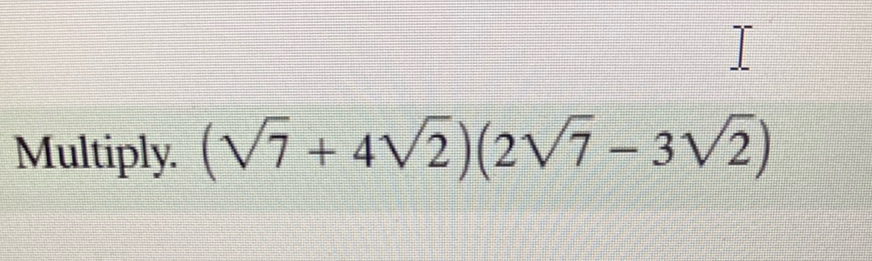Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Multiply. (sqrt7+4sqrt2)(2sqrt7-3sqrt2)

Multiply. (7+42)(27−32) (\sqrt{7}+4 \sqrt{2})(2 \sqrt{7}-3 \sqrt{2})

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Add, subtract, multiply, and divide polynomialsright chevron icon

Full solution

Q. Multiply. (7+42)(27−32) (\sqrt{7}+4 \sqrt{2})(2 \sqrt{7}-3 \sqrt{2})
  1. Identify terms: Step 11: Identify the terms to distribute.\newlineWe have (7+42)(27−32)(\sqrt{7} + 4\sqrt{2})(2\sqrt{7} - 3\sqrt{2}).\newlineDistribute each term in the first parenthesis to each term in the second parenthesis.
  2. Distribute 7\sqrt{7}: Step 22: Distribute 7\sqrt{7} to (27−32)(2\sqrt{7} - 3\sqrt{2}).\newline7×27=2×7=14\sqrt{7} \times 2\sqrt{7} = 2 \times 7 = 14,\newline7×(−32)=−314\sqrt{7} \times (-3\sqrt{2}) = -3\sqrt{14}.
  3. Distribute 424\sqrt{2}: Step 33: Distribute 424\sqrt{2} to (27−32)(2\sqrt{7} - 3\sqrt{2}).42×27=8144\sqrt{2} \times 2\sqrt{7} = 8\sqrt{14},42×(−32)=−12×2=−244\sqrt{2} \times (-3\sqrt{2}) = -12 \times 2 = -24.
  4. Combine terms: Step 44: Combine all terms. 14−314+814−2414 - 3\sqrt{14} + 8\sqrt{14} - 24. Combine like terms: 14+(814−314)−24=14+514−2414 + (8\sqrt{14} - 3\sqrt{14}) - 24 = 14 + 5\sqrt{14} - 24.
  5. Simplify expression: Step 55: Simplify the final expression. \newline14−24=−1014 - 24 = -10,\newlineSo, −10+514-10 + 5\sqrt{14}.

More problems from Add, subtract, multiply, and divide polynomials

Question
Find the degree of this polynomial.\newline`5b^{10} + 3b^3`\newline_______
Get tutor helpright-arrow

Posted 3 months ago

Question
Subtract.\newline(9a+5)−(2a+4)(9a + 5) - (2a + 4)\newline____
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the product. Simplify your answer. \newline−3v2(v2−9)-3v^2(v^2 - 9)\newline________
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the product. Simplify your answer.\newline(v−3)(4v+1)(v - 3)(4v + 1)\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the square. Simplify your answer.\newline(3y+2)2(3y + 2)^2\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. If there is a remainder, include it as a simplified fraction.\newline(24t2+36t)÷6t(24t^2 + 36t) \div 6t\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Is the function q(x)=x6−9 q(x) = x^6 - 9 even, odd, or neither?\newlineChoices:\newline[[even][odd][neither]]\text{[[even][odd][neither]]}
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the product. Simplify your answer. \newline−3q2(−3q2+q)-3q^2(-3q^2 + q)\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the product. Simplify your answer.\newline(r+3)(4r+2)(r + 3)(4r + 2)\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the roots of the factored polynomial.\newline(x+7)(x+4)(x + 7)(x + 4)\newlineWrite your answer as a list of values separated by commas.\newlinex=x = ____
Get tutor helpright-arrow

Posted 3 months ago

View all (448)