Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

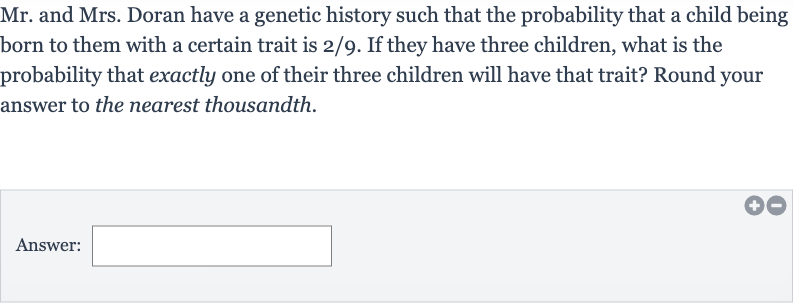
Mr. and Mrs. Doran have a genetic history such that the probability that a child being born to them with a certain trait is 2/9. If they have three children, what is the probability that exactly one of their three children will have that trait? Round your answer to the nearest thousandth. Answer:

Mr. and Mrs. Doran have a genetic history such that the probability that a child being born to them with a certain trait is 22/99. If they have three children, what is the probability that exactly one of their three children will have that trait? Round your answer to the nearest thousandth.\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find probabilities using the binomial distributionright chevron icon

Full solution

Q. Mr. and Mrs. Doran have a genetic history such that the probability that a child being born to them with a certain trait is 22/99. If they have three children, what is the probability that exactly one of their three children will have that trait? Round your answer to the nearest thousandth.\newlineAnswer:
  1. Identify Probability and Events: Identify the probability of a single event and the total number of events. The probability of a child having the trait is 29\frac{2}{9}, and the probability of a child not having the trait is 1−29=791 - \frac{2}{9} = \frac{7}{9}. Since they have 33 children, we will consider three separate events.
  2. Calculate Probability of One Child: Calculate the probability of exactly one child having the trait. The scenario where exactly one child has the trait can occur in three different ways: the first child has the trait and the other two do not, the second child has the trait and the others do not, or the third child has the trait and the others do not. We will calculate the probability for one scenario and then multiply by 33 since each scenario is equally likely.
  3. Calculate Probability for Scenario: Calculate the probability for one scenario.\newlineFor the first child to have the trait and the other two not to have it, we multiply the probabilities of each independent event: (29)×(79)×(79)(\frac{2}{9}) \times (\frac{7}{9}) \times (\frac{7}{9}).
  4. Perform Calculation for Scenario: Perform the calculation for one scenario.\newline(29)×(79)×(79)=29×4981=98729(\frac{2}{9}) \times (\frac{7}{9}) \times (\frac{7}{9}) = \frac{2}{9} \times \frac{49}{81} = \frac{98}{729}.
  5. Multiply Probability by Scenarios: Multiply the probability of one scenario by the number of scenarios.\newlineSince there are three scenarios where exactly one child has the trait, we multiply the result from Step 44 by 33.\newline3×(98729)=2947293 \times (\frac{98}{729}) = \frac{294}{729}.
  6. Simplify Fraction and Round: Simplify the fraction, if possible, and round to the nearest thousandth. \newline294729\frac{294}{729} can be simplified by dividing both the numerator and the denominator by 33.\newline294÷3=98294 \div 3 = 98\newline729÷3=243729 \div 3 = 243\newlineSo, the simplified probability is 98243\frac{98}{243}. To round to the nearest thousandth, we divide 9898 by 243243.\newline98÷243≈0.40398 \div 243 \approx 0.403.

More problems from Find probabilities using the binomial distribution

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 9 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 9 months ago

Question
Y Y is the number of desserts available in a randomly chosen restaurant.\newlineIs the random variable Y Y discrete or continuous?\newlineChoices:\newline[A]discrete \text{[A]discrete} \newline[B]continuous \text{[B]continuous}
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous for all real numbers?\newlineg(x)=ln⁡(x) g(x)=\ln (x) \newlinef(x)=1x f(x)=\frac{1}{x} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newlineD Neither g g nor f f
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous at x=−1 x=-1 ?\newlineg(x)=sin⁡(x+1) g(x)=\sin (x+1) \newlinef(x)=1x−1 f(x)=\frac{1}{x-1} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newline(D) Neither g g nor f f
Get tutor helpright-arrow

Posted 8 months ago

Question
Let g g be a continuous function on the closed interval [−1,4] [-1,4] , where g(−1)=−4 g(-1)=-4 and g(4)=1 g(4)=1 .\newlineWhich of the following is guaranteed by the Intermediate Value Theorem?\newlineChoose 11 answer:\newline(A) g(c)=−3 g(c)=-3 for at least one c c between −1-1 and 44\newline(B) g(c)=3 g(c)=3 for at least one c c between −4-4 and 11\newline(C) g(c)=−3 g(c)=-3 for at least one c c between −4-4 and 11\newline(D) g(c)=3 g(c)=3 for at least one c c between −1-1 and 44
Get tutor helpright-arrow

Posted 8 months ago

View all (89)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant