AI tutor
Full solution
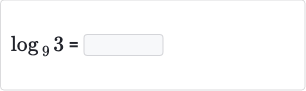
Q.
- Find Logarithm Base: We need to find the value of . This means we are looking for the exponent that must be raised to in order to get .
- Express in Terms of : We know that is squared, i.e., . Therefore, we can express in terms of the base .
- Apply Change of Base Formula: Using the change of base formula for logarithms, we can write as .
- Simplify Using Power Rule: We can simplify by using the power rule of logarithms, which states that . Applying this rule, we get .
- Evaluate : We know that is , because raised to the power of is .
- Substitute and Simplify: Substituting the value we found in the previous step, we get , which simplifies to .
- Final Result: Therefore, .
More problems from Relationship between squares and square roots
QuestionGet tutor help