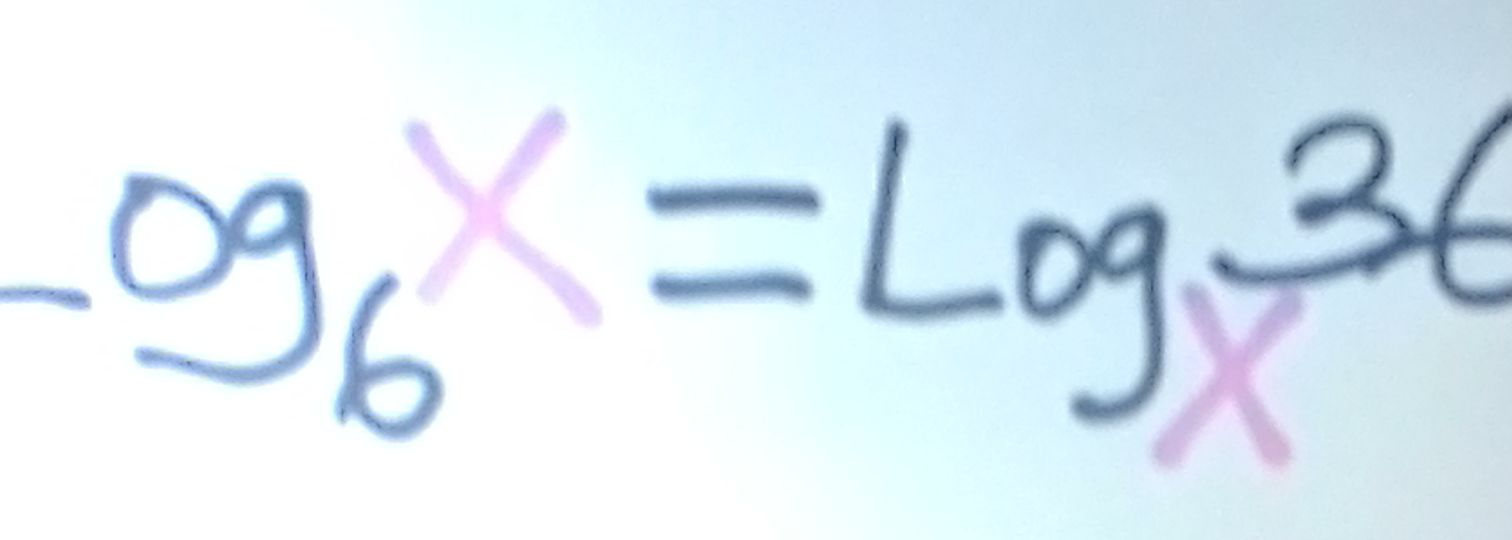Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(6)x=log_(x)36

Solve for $x$ $\newline$ $\log _{6} x=\log _{x} 36$

View step-by-step help

View step-by-step help

Convert between exponential and logarithmic form

Full solution

Q. Solve for

x

\newline

\log _{6} x=\log _{x} 36

Set up equation: Step $1$ : Set up the equation. $\newline$ We have $\log_{6}x = \log_{x}36$ . This means $6$ raised to some power equals $x$ , and $x$ raised to some power equals $36$ .
Convert to exponential form: Step $2$ : Convert the logarithmic equation to an exponential form. $\newline$ $6^a = x$ and $x^b = 36$ , where $a = \log_{6}x$ and $b = \log_{x}36$ .
Substitute and simplify: Step $3$ : Substitute $x$ from the first equation into the second equation. $\newline$ $(6^a)^b = 36$ $\newline$ $6^{ab} = 36$
Recognize $36$ as power of $6$ : Step $4$ : Recognize that $36$ can be written as a power of $6$ . $\newline$ $36 = 6^2$
Set exponents equal: Step $5$ : Set the exponents equal to each other since the bases are the same. $a^b = 2$
Solve for $x$ : Step $6$ : Solve for $x$ using the first equation. $\newline$ Since $a = \log_{6}x$ , we know $6^a = x$ . $\newline$ From $ab = 2$ and knowing $b = \log_{x}36$ , we can substitute $b = \frac{2}{a}$ into the equation. $\newline$ $a*\left(\frac{2}{a}\right) = 2$ $\newline$ $2 = 2$ $\newline$ $a = 1$

More problems from Convert between exponential and logarithmic form

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago