AI tutor
Full solution
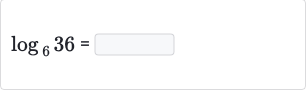
Q.
- Identify Base and Argument: Identify the base and the argument of the logarithm.The base of the logarithm is , and the argument is .
- Express as Power of : Express as a power of . is squared, which means .
- Rewrite Using Power: Rewrite the logarithm using the argument expressed as a power of the base. becomes .
- Apply Power Property: Apply the power property of logarithms. The power property states that . Therefore, is .
- Evaluate Logarithm: Evaluate . The logarithm of a number to the same base is always . Therefore, is .
- Multiply Result: Multiply the result from Step by the exponent from Step . is , which equals .
More problems from Evaluate logarithms using properties
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help