AI tutor
Full solution
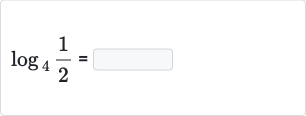
Q.
- Express Quotient Logarithm: We need to express the logarithm of a quotient in terms of the logarithms of the numerator and the denominator.The logarithm of a quotient rule states that is equal to .Therefore, can be written as .
- Evaluate Log : Now we need to evaluate . The logarithm of any number at its own base is , so is . Since is the multiplicative identity, is .
- Evaluate Log : Next, we need to evaluate . We know that is squared, so we can express as . Therefore, is asking us for what power we need to raise to get . Since is squared, we need to raise to the power of to get . So, is .
- Combine Results: Now we can combine our results to find the final answer.We have equals , which is .Therefore, is .