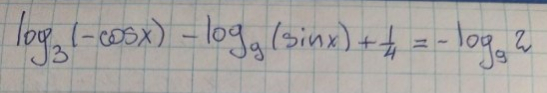Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(3)(-cos x)-log_(9)(sin x)+(1)/(4)=-log_(9)2

log⁡3(−cos⁡x)−log⁡9(sin⁡x)+14=−log⁡92 \log _{3}(-\cos x)-\log _{9}(\sin x)+\frac{1}{4}=-\log _{9} 2

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Quotient property of logarithmsright chevron icon

Full solution

Q. log⁡3(−cos⁡x)−log⁡9(sin⁡x)+14=−log⁡92 \log _{3}(-\cos x)-\log _{9}(\sin x)+\frac{1}{4}=-\log _{9} 2
  1. Convert to Base 33: Convert the base of the second logarithm from base 99 to base 33 using the change of base formula: log⁡b(a)=log⁡c(a)log⁡c(b)\log_b(a) = \frac{\log_c(a)}{\log_c(b)}.\newlineCalculation: log⁡9(sin⁡x)=log⁡3(sin⁡x)log⁡3(9)\log_{9}(\sin x) = \frac{\log_{3}(\sin x)}{\log_{3}(9)}\newlineSince log⁡3(9)=2\log_{3}(9) = 2, it simplifies to log⁡9(sin⁡x)=12∗log⁡3(sin⁡x)\log_{9}(\sin x) = \frac{1}{2} * \log_{3}(\sin x).
  2. Substitute Converted Logarithm: Substitute the converted logarithm back into the original equation.\newlineCalculation: log⁡3(−cos⁡x)−12⋅log⁡3(sin⁡x)+14=−log⁡9(2)\log_{3}(-\cos x) - \frac{1}{2} \cdot \log_{3}(\sin x) + \frac{1}{4} = -\log_{9}(2)
  3. Convert to Base 33: Convert −log⁡9(2)-\log_{9}(2) to base 33 using the same change of base formula.\newlineCalculation: −log⁡9(2)=−log⁡3(2)log⁡3(9)-\log_{9}(2) = -\frac{\log_{3}(2)}{\log_{3}(9)}\newlineSince log⁡3(9)=2\log_{3}(9) = 2, it simplifies to −log⁡9(2)=−(12)⋅log⁡3(2)-\log_{9}(2) = -\left(\frac{1}{2}\right) \cdot \log_{3}(2).
  4. Combine Terms in Base 33: Combine all terms in base 33.\newlineCalculation: log⁡3(−cos⁡x)−12⋅log⁡3(sin⁡x)+14=−12⋅log⁡3(2)\log_{3}(-\cos x) - \frac{1}{2} \cdot \log_{3}(\sin x) + \frac{1}{4} = -\frac{1}{2} \cdot \log_{3}(2)
  5. Isolate Logarithm: Attempt to isolate log⁡3(−cos⁡x)\log_{3}(-\cos x).\newlineCalculation: log⁡3(−cos⁡x)=12⋅log⁡3(sin⁡x)−14+12⋅log⁡3(2)\log_{3}(-\cos x) = \frac{1}{2} \cdot \log_{3}(\sin x) - \frac{1}{4} + \frac{1}{2} \cdot \log_{3}(2)

More problems from Quotient property of logarithms

Question
Solve. Write your answer as an integer or a fraction in simplest form.\newline5x=15^x=1\newlinex=x= _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Steven opened a savings account and deposited $100.00\$100.00 as principal. The account earns 9%9\% interest, compounded annually. What is the balance after 55 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.\newline$\$____
Get tutor helpright-arrow

Posted 2 months ago

Question
Use the following function rule to find f(1) f(1) .\newlinef(x)=12(7)x+8 f(x) = 12(7)^x + 8 \newlinef(1)= f(1) = _____
Get tutor helpright-arrow

Posted 1 month ago

Question
The town of Valley View conducted a census this year, which showed that it has a population of 1,8001,800 people. Based on the census data, it is estimated that the population of Valley View will grow by 12%12\% each decade.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the town population, yy, xx decades after this census was taken.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=9x7 = 9^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=ex7 = e^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve. Simplify your answer.\newlinelog⁡u=1\log u = 1\newlineu=u = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Simplify your answer.\newline7log⁡x=77\log x = 7\newlinex=x = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
How does g(t)=3t g(t) = 3^t change over the interval from t=3 t = 3 to t=4 t = 4 ?\newlineChoices:\newline(A) g(t) g(t) decreases by 3 3 \newline(B) g(t) g(t) increases by 3 3 \newline(C) g(t) g(t) decreases by 3% 3\%\newline(D) g(t) g(t) increases by 200%200\%
Get tutor helpright-arrow

Posted 2 months ago

Question
A function f(x) f(x) increases by 6 6 over every unit interval in x x and f(0)=0 f(0) = 0 .\newlineWhich could be a function rule for f(x) f(x) ?\newlineChoices:\newline(A) f(x)=6xf(x) = 6^x\newline(B) f(x)=6xf(x) = 6x\newline(C) f(x)=16xf(x) = \frac{1}{6^x}\newline(D) f(x)=x6f(x) = \frac{x}{6}
Get tutor helpright-arrow

Posted 2 months ago

View all (136)