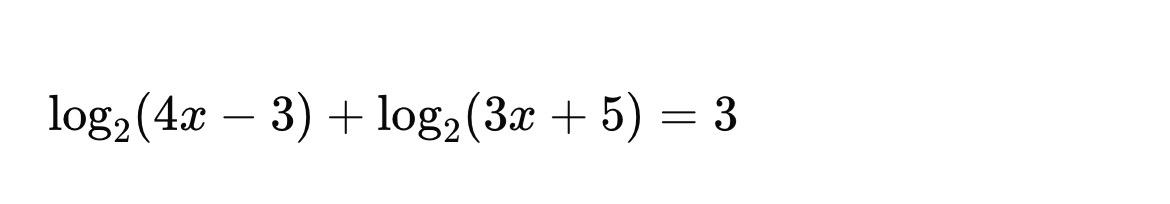log_(2)(4x-3)+log_(2)(3x+5)=3

Question

Bytelearn · Accepted Answer

Combine Logs: Use the property of logarithms that allows us to combine the two log terms on the left side of the equation into a single log term by multiplication. log₂(4x-3) + log₂(3x+5) = log₂((4x-3)(3x+5))Exponential Form: Since the sum of the logs is equal to 3, we can rewrite the equation in exponential form to remove the logarithm. log₂((4x-3)(3x+5)) = 3 is equivalent to 2³ = (4x-3)(3x+5)Calculate Value: Calculate the value of 2³. 2³ = 8Set Product Equal: Set the product of the binomials equal to 8. (4x-3)(3x+5) = 8Expand Equation: Expand the left side of the equation using the distributive property (FOIL method). 4x(3x) + 4x(5) - 3(3x) - 3(5) = 8 12x² + 20x - 9x - 15 = 8Combine Like Terms: Combine like terms on the left side of the equation. 12x² + 20x - 9x - 15 = 8 12x² + 11x - 15 = 8Set Equation to Zero: Subtract 8 from both sides to set the equation to zero. 12x² + 11x - 15 - 8 = 0 12x² + 11x - 23 = 0Quadratic Formula: Factor the quadratic equation or use the quadratic formula to find the values of x. This equation does not factor nicely, so we will use the quadratic formula. x = [-b ± √(b²-4ac)] / (2a) where a = 12, b = 11, and c = -23.Calculate Discriminant: Calculate the discriminant (b²-4ac). Discriminant = 11² - 4(12)(-23) Discriminant = 121 + 1104 Discriminant = 1225Calculate Solutions: Since the discriminant is positive, there are two real solutions. Calculate the solutions using the quadratic formula. x = [-11 ± √1225] / (2*12) x = [-11 ± 35] / 24Check Validity: Calculate the two possible values for x. x₁ = (-11 + 35) / 24 x₁ = 24 / 24 x₁ = 1  x₂ = (-11 - 35) / 24 x₂ = -46 / 24 x₂ = -23/12Check the solutions in the original equation to ensure they do not result in the logarithm of a negative number or zero, as the logarithm is not defined for these values. For x₁ = 1: log₂(4(1)-3) + log₂(3(1)+5) = log₂(4-3) + log₂(3+5) = log₂(1) + log₂(8) = 0 + 3 = 3 This is valid.  For x₂ = -23/12: log₂(4(-23/12)-3) + log₂(3(-23/12)+5) involves the logarithm of negative numbers, which is not defined. This is not valid.  Therefore, x₂ = -23/12 is not a valid solution.

$\log_{2}(4x-3)+\log_{2}(3x+5)=3$

Full solution

More problems from Solve multi-step equations with fractional coefficients

Related topics

log⁡2(4x−3)+log⁡2(3x+5)=3\log_{2}(4x-3)+\log_{2}(3x+5)=3log2​(4x−3)+log2​(3x+5)=3

$\log_{2}(4x-3)+\log_{2}(3x+5)=3$