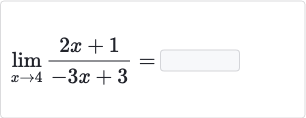AI tutor
Full solution
Q.
- Identify Limit Form: Identify the form of the limit as approaches . We substitute with in the expression to see if the limit can be directly calculated. . Since we get a determinate form (not or ), we can conclude that the limit is .
- Substitute with : Conclude the limit based on the calculation from Step .Since we obtained a numerical value in Step , we can conclude that the limit of as approaches is .