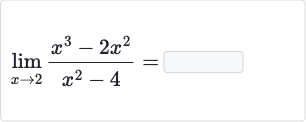lim_(x rarr2)(x^(3)-2x^(2))/(x^(2)-4)=

Question

Bytelearn · Accepted Answer

Given Limit Problem: We are given the limit problem: lim_(x -> 2)(x^3 - 2x^2) / (x^2 - 4) First, let's try to directly substitute x = 2 into the expression to see if it yields a determinate form. Substituting x = 2 gives us: (2^3 - 2*2^2) / (2^2 - 4) = (8 - 8) / (4 - 4) = 0/0 This is an indeterminate form, so we cannot find the limit by direct substitution.Direct Substitution: Since we have an indeterminate form of 0/0, we should look for a way to simplify the expression. We can factor the numerator and the denominator. The numerator x^3 - 2x^2 can be factored as x^2(x - 2). The denominator x^2 - 4 is a difference of squares and can be factored as (x + 2)(x - 2). Now we rewrite the limit expression with the factored terms: lim_(x -> 2)(x^2(x - 2)) / ((x + 2)(x - 2))Factorization: We notice that (x - 2) is a common factor in both the numerator and the denominator. We can cancel this common factor out: lim_(x -> 2)(x^2) / (x + 2) Now, we can try to directly substitute x = 2 into this simplified expression.Cancellation: Substituting x = 2 into the simplified expression gives us: (2^2) / (2 + 2) = 4 / 4 = 1 This is the value of the limit as x approaches 2.

$\lim _{x \rightarrow 2} \frac{x^{3}-2 x^{2}}{x^{2}-4}=$

Full solution

More problems from Factor sums and differences of cubes

Related topics

lim⁡x→2x3−2x2x2−4= \lim _{x \rightarrow 2} \frac{x^{3}-2 x^{2}}{x^{2}-4}= limx→2​x2−4x3−2x2​=

$\lim _{x \rightarrow 2} \frac{x^{3}-2 x^{2}}{x^{2}-4}=$