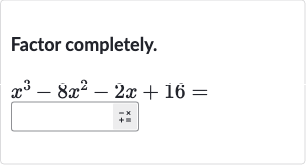Factor completely. $\newline$ $x^{3}-8 x^{2}-2 x+16=$

View step-by-step help

Home

Math Problems

Algebra 2

Factor polynomials

Full solution

Q. Factor completely.

\newline

x^{3}-8 x^{2}-2 x+16=

Identify Terms: Step Title: Identify the Terms $\newline$ Concise Step Description: Identify the terms of the polynomial to understand its structure. $\newline$ Step Calculation: The polynomial is $x^3 - 8x^2 - 2x + 16$ , which has four terms. $\newline$ Step Output: Terms: $x^3$ , $-8x^2$ , $-2x$ , $+16$
Group Terms: Step Title: Group the Terms $\newline$ Concise Step Description: Group the terms in pairs to facilitate factoring by grouping. $\newline$ Step Calculation: Group the terms as $(x^3 - 8x^2)$ and $(-2x + 16)$ . $\newline$ Step Output: Grouped Terms: $(x^3 - 8x^2)$ , $(-2x + 16)$
Factor by Grouping: Step Title: Factor by Grouping $\newline$ Concise Step Description: Factor out the greatest common factor from each group. $\newline$ Step Calculation: From $x^3 - 8x^2$ , factor out $x^2$ to get $x^2(x - 8)$ . From $-2x + 16$ , factor out $-2$ to get $-2(x - 8)$ . $\newline$ Step Output: Factored Groups: $x^2(x - 8)$ , $-2(x - 8)$
Factor Out Common Binomial: Step Title: Factor Out the Common Binomial $\newline$ Concise Step Description: Factor out the common binomial factor from the factored groups. $\newline$ Step Calculation: The common binomial factor is $(x - 8)$ . Factoring it out, we get $(x - 8)(x^2 - 2)$ . $\newline$ Step Output: Factored Form: $(x - 8)(x^2 - 2)$
Check for Further Factoring: Step Title: Check for Further Factoring $\newline$ Concise Step Description: Check if the remaining quadratic can be factored further. $\newline$ Step Calculation: The quadratic $x^2 - 2$ is a difference of squares and can be factored as $(x + \sqrt{2})(x - \sqrt{2})$ . $\newline$ Step Output: Further Factored Form: $(x - 8)(x + \sqrt{2})(x - \sqrt{2})$