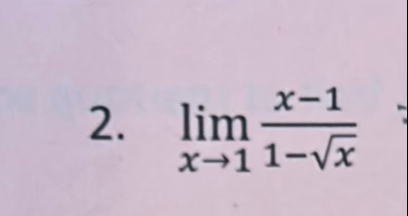Evaluate the limit: lim_(x rarr1)(x-1)/(1-sqrtx)

Question

Bytelearn · Accepted Answer

Identify indeterminate form: Identify the indeterminate form. We need to check if the expression (x-1)/(1-sqrt(x)) results in an indeterminate form when x approaches 1. Substitute x = 1 into the expression to see if it results in 0/0. (1-1)/(1-sqrt(1)) = 0/0. Since we get 0/0, it is an indeterminate form.Simplify expression: Simplify the expression to resolve the indeterminate form. We can use algebraic manipulation to simplify the expression. One common technique is to multiply the numerator and the denominator by the conjugate of the denominator. The conjugate of (1-sqrt(x)) is (1+sqrt(x)). Multiply both the numerator and denominator by this conjugate. ((x-1)/(1-sqrt(x))) * ((1+sqrt(x))/(1+sqrt(x))) = ((x-1)*(1+sqrt(x)))/((1-sqrt(x))*(1+sqrt(x))).Perform multiplication: Perform the multiplication in the numerator and denominator. Expand the numerator: (x-1)*(1+sqrt(x)) = x + x*sqrt(x) - 1 - sqrt(x). Expand the denominator using the difference of squares: (1-sqrt(x))*(1+sqrt(x)) = 1 - (sqrt(x))^2 = 1 - x. Now the expression is ((x + x*sqrt(x) - 1 - sqrt(x))/(1 - x)).Further simplify expression: Simplify the expression further. Notice that the terms in the numerator can be rearranged to cancel out with the denominator. Rearrange the numerator: (x - 1) + x*sqrt(x) - sqrt(x) = (x - 1) - (sqrt(x) - x*sqrt(x)). Now the expression is ((x - 1) - (sqrt(x) - x*sqrt(x)))/(1 - x).Factor out common terms: Factor out common terms to cancel them. Factor (x - 1) out of the numerator: (x - 1)(1 - sqrt(x)). Now the expression is ((x - 1)(1 - sqrt(x)))/(1 - x). Since (x - 1) is equivalent to -(1 - x), we can cancel out (1 - x) in the numerator and denominator. The expression simplifies to -(1 - sqrt(x)).Take limit: Take the limit of the simplified expression as x approaches 1. Now that we have a simplified expression, we can substitute x = 1 directly. lim_(x -> 1) -(1 - sqrt(x)) = -(1 - sqrt(1)) = -(1 - 1) = 0.

Evaluate the limit: $\lim _{x \rightarrow 1} \frac{x-1}{1-\sqrt{x}}$

Full solution

More problems from Dilations of functions

Related topics

Evaluate the limit: lim⁡x→1x−11−x \lim _{x \rightarrow 1} \frac{x-1}{1-\sqrt{x}} limx→1​1−x​x−1​

Evaluate the limit: $\lim _{x \rightarrow 1} \frac{x-1}{1-\sqrt{x}}$