Full solution
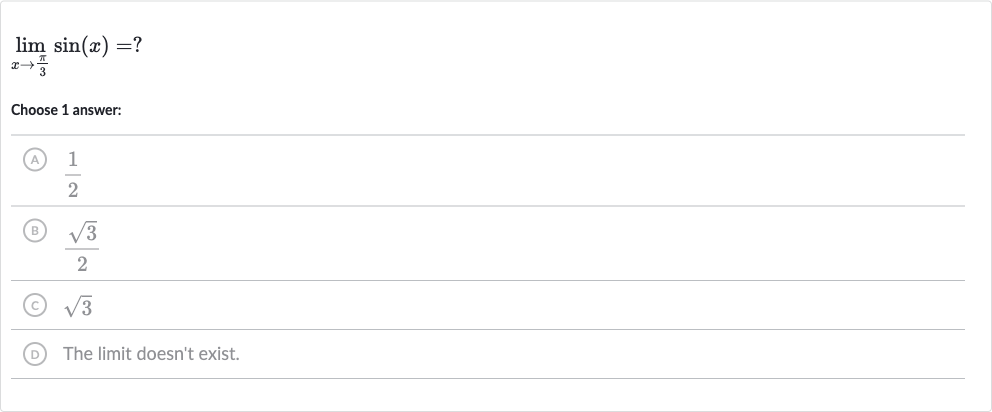
Q. Choose answer:(A) (B) (C) (D) The limit doesn't exist.
- Identify the function: Identify the function whose limit needs to be found.We need to find the limit of as approaches .
- Determine continuity: Determine if the function is continuous at the point . The sine function is continuous everywhere on the real number line, including at .
- Evaluate at : Evaluate the function at the point . Since the sine function is continuous at , we can find the limit by direct substitution.
- Conclude the limit: Conclude the limit based on the calculation.The limit of as approaches is .
More problems from Solve quadratic inequalities
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help