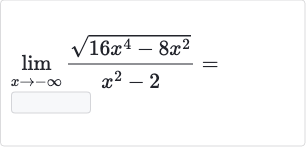AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Full solution
Q.
- Factor Out Highest Power: To find the limit of the given function as approaches negative infinity, we first need to simplify the expression to a form that will allow us to evaluate the limit directly. We can start by factoring out the highest power of in the numerator.
- Simplify Square Root: Factor out from the square root in the numerator to simplify the expression inside the square root.Since , we have:
- Rewrite Limit Expression: Now we can rewrite the original limit expression using the simplified form of the numerator:
- Divide by : Next, we divide both the numerator and the denominator by , the highest power of in the denominator, to simplify the expression further.\lim_{x \to -\infty}\left(\frac{x^\(2\) \sqrt{\(16\) - \frac{\(8\)}{x^\(2\)}}}{x^\(2\) - \(2\)}\right) = \lim_{x \to -\infty}\left(\frac{\sqrt{\(16\) - \frac{\(8\)}{x^\(2\)}}}{\(1\) - \frac{\(2\)}{x^\(2\)}}\right)
- Simplify Further: As \(x\) approaches negative infinity, the terms \(\frac{8}{x^2}\) and \(\frac{2}{x^2}\) in the expression will approach \(0\). Therefore, we can simplify the expression to:\(\newline\)\[\lim_{x \to -\infty}\left(\frac{\sqrt{16 - \frac{8}{x^2}}}{1 - \frac{2}{x^2}}\right) = \lim_{x \to -\infty}\left(\frac{\sqrt{16}}{1}\right)
- Final Limit Calculation: Since the square root of is , and the denominator is , the limit simplifies to:
More problems from Relationship between squares and square roots
QuestionGet tutor help