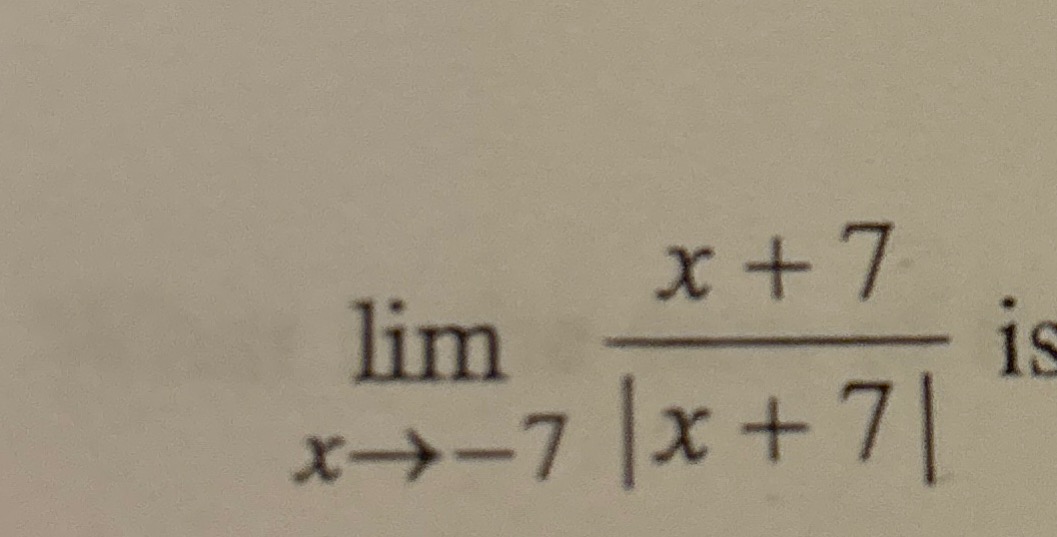Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

lim_(x rarr-7)(x+7)/(|x+7|)

$\lim _{x \rightarrow-7} \frac{x+7}{|x+7|}$

View step-by-step help

View step-by-step help

Add, subtract, multiply, and divide polynomials

Full solution

Q.

\lim _{x \rightarrow-7} \frac{x+7}{|x+7|}

Understand Expression Behavior: Understand the expression and its behavior near $x = -7$ . We need to evaluate the limit of $\frac{x+7}{|x+7|}$ as $x$ approaches $-7$ . Notice that the expression involves an absolute value, which affects the calculation depending on whether $x$ is less than or greater than $-7$ .
Left Side Limit Calculation: Consider the limit from the left side $x$ approaching $-7$ from values less than $-7$ . When $x$ is slightly less than $-7$ , $x+7$ is slightly negative. Therefore, $|x+7| = -(x+7)$ , and the expression becomes: $\frac{x+7}{-(x+7)} = -1$ .
Right Side Limit Calculation: Consider the limit from the right side $x$ approaching $-7$ from values greater than $-7$ . When $x$ is slightly more than $-7$ , $x+7$ is slightly positive. Therefore, $|x+7| = x+7$ , and the expression becomes: $\frac{x+7}{x+7} = 1$ .
Comparison of Limits: Compare the two one-sided limits. $\newline$ The left-hand limit as $x$ approaches $-7$ is $-1$ , and the right-hand limit as $x$ approaches $-7$ is $1$ . Since these two limits are not equal, the overall limit does not exist.

More problems from Add, subtract, multiply, and divide polynomials

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 2 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 1 month ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 2 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 2 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 2 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 2 months ago