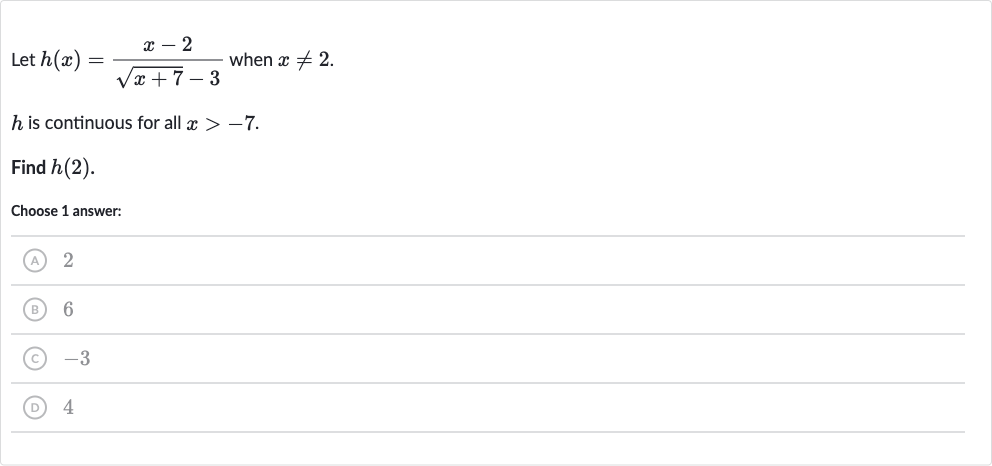
Let h(x)=(x-2)/(sqrt(x+7)-3) when x!=2. h is continuous for all x -7. Find h(2). Choose 1 answer: (A) 2 (B) 6 (C) -3 (D) 4

Question

Let  h(x)=(x-2)/(sqrt(x+7)-3) when  x!=2.  h is continuous for all  x > -7. Find  h(2). Choose 1 answer: (A) 2 (B) 6 (C) -3 (D) 4

Bytelearn · Accepted Answer

Recognize the undefined point: Recognize that the function h(x) is not defined at x = 2 because it would result in a division by zero. However, we are asked to find the limit as x approaches 2, which will give us the continuous value of h(x) at x = 2.Rationalize the denominator: To find the limit of h(x) as x approaches 2, we can use the conjugate of the denominator to rationalize it. Multiply the numerator and the denominator by the conjugate of the denominator, which is (sqrt(x+7)+3).Multiply numerator and denominator: Perform the multiplication from Step 2: h(x) = [(x-2)(sqrt(x+7)+3)] / [(sqrt(x+7)-3)(sqrt(x+7)+3)]Simplify the denominator: Simplify the denominator using the difference of squares formula: Denominator = (sqrt(x+7))^2 - (3)^2 = x + 7 - 9 = x - 2Simplify the numerator: Simplify the numerator by distributing (x-2) to (sqrt(x+7)+3): Numerator = x*sqrt(x+7) + 3x - 2*sqrt(x+7) - 6Cancel out common terms: Notice that the denominator (x - 2) cancels out with the (x - 2) term in the numerator, leaving us with: h(x) = (sqrt(x+7) + 3)Substitute x = 2: Now, substitute x = 2 into the simplified h(x) to find h(2): h(2) = sqrt(2+7) + 3 = sqrt(9) + 3 = 3 + 3 = 6

Let $h(x)=\frac{x-2}{\sqrt{x+7}-3}$ when $x \neq 2$ . $\newline$ $h$ is continuous for all x>-7 . $\newline$ Find $h(2)$ . $\newline$ Choose $1$ answer: $\newline$ (A) $2$ $\newline$ (B) $6$ $\newline$ (C) $-3$ $\newline$ (D) $4$

Full solution

More problems from Conjugate root theorems

Related topics

Let h(x)=x−2x+7−3 h(x)=\frac{x-2}{\sqrt{x+7}-3} h(x)=x+7​−3x−2​ when x≠2 x \neq 2 x=2.\newlineh h h is continuous for all x>-7 .\newlineFind h(2) h(2) h(2).\newlineChoose 111 answer:\newline(A) 222\newline(B) 666\newline(C) −3-3−3\newline(D) 444

Let $h(x)=\frac{x-2}{\sqrt{x+7}-3}$ when $x \neq 2$ . $\newline$ $h$ is continuous for all x>-7 . $\newline$ Find $h(2)$ . $\newline$ Choose $1$ answer: $\newline$ (A) $2$ $\newline$ (B) $6$ $\newline$ (C) $-3$ $\newline$ (D) $4$