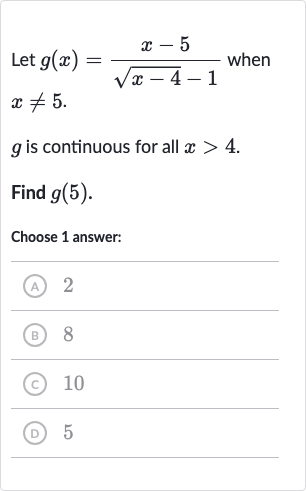
Let g(x)=(x-5)/(sqrt(x-4)-1) when x!=5. g is continuous for all x 4. Find g(5). Choose 1 answer: (A) 2 (B) 8 (C) 10 (D) 5

Question

Let  g(x)=(x-5)/(sqrt(x-4)-1) when  x!=5.  g is continuous for all  x > 4. Find  g(5). Choose 1 answer: (A) 2 (B) 8 (C) 10 (D) 5

Bytelearn · Accepted Answer

Define Limit of g(5): To find the value of g(5), we need to evaluate the limit of g(x) as x approaches 5, because g(x) is not defined at x = 5 but is continuous for all x > 4. This suggests that we should use the limit process to find g(5).Simplify Expression by Conjugate: We can simplify the expression for g(x) by multiplying the numerator and denominator by the conjugate of the denominator to eliminate the square root in the denominator. The conjugate of sqrt(x-4)-1 is sqrt(x-4)+1.Multiply Numerator and Denominator: Multiplying the numerator and denominator by the conjugate, we get: g(x) = [(x-5)(sqrt(x-4)+1)] / [(sqrt(x-4)-1)(sqrt(x-4)+1)]Simplify Denominator: Simplifying the denominator using the difference of squares, we get: g(x) = [(x-5)(sqrt(x-4)+1)] / [(x-4) - 1]Further Simplify Denominator: Further simplifying the denominator, we get: g(x) = [(x-5)(sqrt(x-4)+1)] / [x-5]Cancel Out Common Term: We can now cancel out the (x-5) term in the numerator and denominator, as long as x is not equal to 5. This is valid because we are interested in the limit as x approaches 5, not the value at x = 5.Final Simplified Expression: After canceling out the (x-5) term, we are left with: g(x) = sqrt(x-4) + 1Substitute x = 5: Now we can safely substitute x = 5 into the simplified expression to find g(5): g(5) = sqrt(5-4) + 1Calculate Final Value: Calculating the square root and adding 1, we get: g(5) = sqrt(1) + 1 = 1 + 1 = 2

Let $g(x)=\frac{x-5}{\sqrt{x-4}-1}$ when $x \neq 5$ . $\newline$ $g$ is continuous for all x>4 . $\newline$ Find $g(5)$ . $\newline$ Choose $1$ answer: $\newline$ (A) $2$ $\newline$ (B) $8$ $\newline$ (C) $10$ $\newline$ (D) $5$

Full solution

More problems from Conjugate root theorems

Related topics

Let g(x)=x−5x−4−1 g(x)=\frac{x-5}{\sqrt{x-4}-1} g(x)=x−4​−1x−5​ when x≠5 x \neq 5 x=5.\newlineg g g is continuous for all x>4 .\newlineFind g(5) g(5) g(5).\newlineChoose 111 answer:\newline(A) 222\newline(B) 888\newline(C) 101010\newline(D) 555

Let $g(x)=\frac{x-5}{\sqrt{x-4}-1}$ when $x \neq 5$ . $\newline$ $g$ is continuous for all x>4 . $\newline$ Find $g(5)$ . $\newline$ Choose $1$ answer: $\newline$ (A) $2$ $\newline$ (B) $8$ $\newline$ (C) $10$ $\newline$ (D) $5$