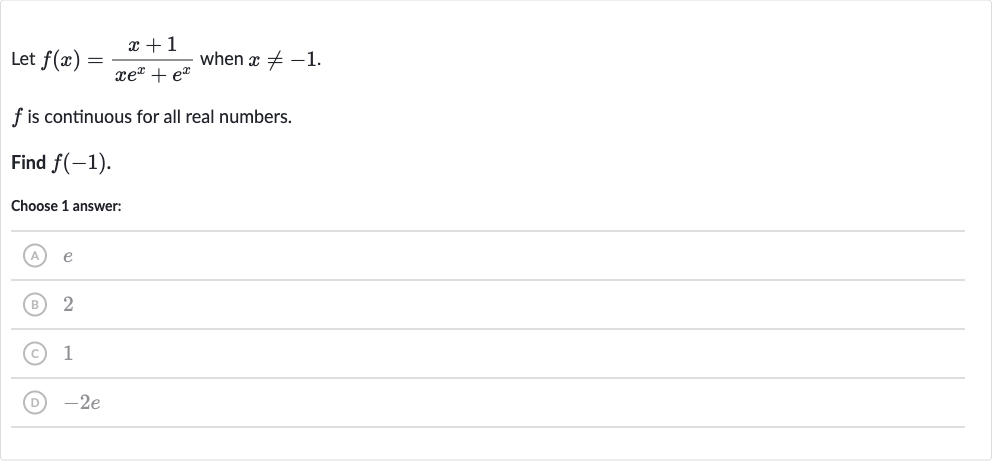
Let f(x)=(x+1)/(xe^(x)+e^(x)) when x!=-1. f is continuous for all real numbers. Find f(-1). Choose 1 answer: (A) e (B) 2 (C) 1 (D) -2e

Question

Let  f(x)=(x+1)/(xe^(x)+e^(x)) when  x!=-1.  f is continuous for all real numbers. Find  f(-1). Choose 1 answer: (A)  e (B) 2 (C) 1 (D)  -2e

Bytelearn · Accepted Answer

Finding f(-1): We need to find the value of f(-1). However, we cannot directly substitute x = -1 into the function because the function is not defined at x = -1. We will use the limit process to find the value of f(x) as x approaches -1.Using the limit process: Let's consider the limit of f(x) as x approaches -1: lim (x -> -1) f(x) = lim (x -> -1) (x+1)/(xe^(x)+e^(x))Applying L'Hôpital's Rule: We can see that if we substitute x = -1 directly, we get 0/0, which is an indeterminate form. To resolve this, we can apply L'Hôpital's Rule, which states that if the limit of f(x)/g(x) as x approaches a value c is an indeterminate form 0/0 or ∞/∞, then the limit is the same as the limit of the derivatives of the numerator and the denominator, provided that the limit exists.Finding the derivatives: We will find the derivatives of the numerator and the denominator separately. The derivative of the numerator (x+1) with respect to x is 1. The derivative of the denominator (xe^(x)+e^(x)) with respect to x is e^(x) + xe^(x) + e^(x) using the product rule and the fact that the derivative of e^(x) is e^(x).Substituting x = -1: Now we apply L'Hôpital's Rule: lim (x -> -1) f(x) = lim (x -> -1) (1)/(e^(x) + xe^(x) + e^(x))Simplifying the expression: We substitute x = -1 into the derivatives to find the limit: lim (x -> -1) (1)/(e^(x) + xe^(x) + e^(x)) = (1)/(e^(-1) + (-1)e^(-1) + e^(-1))Final result: Simplify the expression: (1)/(e^(-1) - e^(-1) + e^(-1)) = (1)/(e^(-1))Since e^(-1) is the same as 1/e, we can rewrite the expression as: (1)/(1/e) = e

Let $f(x)=\frac{x+1}{x e^{x}+e^{x}}$ when $x \neq-1$ . $\newline$ $f$ is continuous for all real numbers. $\newline$ Find $f(-1)$ . $\newline$ Choose $1$ answer: $\newline$ (A) $e$ $\newline$ (B) $2$ $\newline$ (C) $1$ $\newline$ (D) $-2 e$

Full solution

More problems from Conjugate root theorems

Related topics

Let f(x)=x+1xex+ex f(x)=\frac{x+1}{x e^{x}+e^{x}} f(x)=xex+exx+1​ when x≠−1 x \neq-1 x=−1.\newlinef f f is continuous for all real numbers.\newlineFind f(−1) f(-1) f(−1).\newlineChoose 111 answer:\newline(A) e e e\newline(B) 222\newline(C) 111\newline(D) −2e -2 e −2e

Let $f(x)=\frac{x+1}{x e^{x}+e^{x}}$ when $x \neq-1$ . $\newline$ $f$ is continuous for all real numbers. $\newline$ Find $f(-1)$ . $\newline$ Choose $1$ answer: $\newline$ (A) $e$ $\newline$ (B) $2$ $\newline$ (C) $1$ $\newline$ (D) $-2 e$