Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

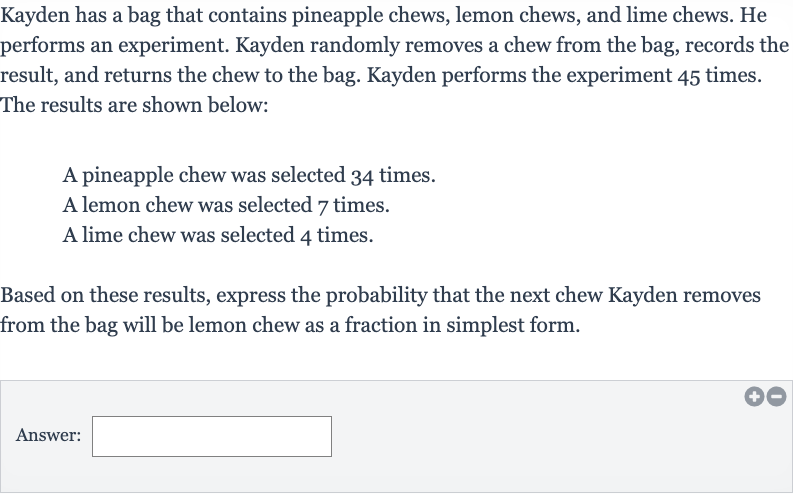
Kayden has a bag that contains pineapple chews, lemon chews, and lime chews. He performs an experiment. Kayden randomly removes a chew from the bag, records the result, and returns the chew to the bag. Kayden performs the experiment 45 times. The results are shown below: A pineapple chew was selected 34 times. A lemon chew was selected 7 times. A lime chew was selected 4 times. Based on these results, express the probability that the next chew Kayden removes from the bag will be lemon chew as a fraction in simplest form. Answer:

Kayden has a bag that contains pineapple chews, lemon chews, and lime chews. He performs an experiment. Kayden randomly removes a chew from the bag, records the result, and returns the chew to the bag. Kayden performs the experiment 4545 times. The results are shown below:\newlineA pineapple chew was selected 3434 times.\newlineA lemon chew was selected 77 times.\newlineA lime chew was selected 44 times.\newlineBased on these results, express the probability that the next chew Kayden removes from the bag will be lemon chew as a fraction in simplest form.\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find probabilities using the binomial distributionright chevron icon

Full solution

Q. Kayden has a bag that contains pineapple chews, lemon chews, and lime chews. He performs an experiment. Kayden randomly removes a chew from the bag, records the result, and returns the chew to the bag. Kayden performs the experiment 4545 times. The results are shown below:\newlineA pineapple chew was selected 3434 times.\newlineA lemon chew was selected 77 times.\newlineA lime chew was selected 44 times.\newlineBased on these results, express the probability that the next chew Kayden removes from the bag will be lemon chew as a fraction in simplest form.\newlineAnswer:
  1. Calculate Probability: To find the probability of selecting a lemon chew, we need to divide the number of times a lemon chew was selected by the total number of chews selected.
  2. Identify Lemon Chews: The number of times a lemon chew was selected is given as 77.
  3. Total Chews Selected: The total number of chews selected is the sum of all the chews selected, which is 3434 (pineapple) + 77 (lemon) + 44 (lime) = 4545.
  4. Calculate Fraction: Now we calculate the probability of selecting a lemon chew as a fraction: Probability = Number of lemon chews selected / Total number of chews selected = 745\frac{7}{45}.
  5. Simplify Fraction: We check if the fraction 745\frac{7}{45} can be simplified. Since 77 and 4545 have no common factors other than 11, the fraction is already in its simplest form.

More problems from Find probabilities using the binomial distribution

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 9 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 9 months ago

Question
Y Y is the number of desserts available in a randomly chosen restaurant.\newlineIs the random variable Y Y discrete or continuous?\newlineChoices:\newline[A]discrete \text{[A]discrete} \newline[B]continuous \text{[B]continuous}
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous for all real numbers?\newlineg(x)=ln⁡(x) g(x)=\ln (x) \newlinef(x)=1x f(x)=\frac{1}{x} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newlineD Neither g g nor f f
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous at x=−1 x=-1 ?\newlineg(x)=sin⁡(x+1) g(x)=\sin (x+1) \newlinef(x)=1x−1 f(x)=\frac{1}{x-1} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newline(D) Neither g g nor f f
Get tutor helpright-arrow

Posted 8 months ago

Question
Let g g be a continuous function on the closed interval [−1,4] [-1,4] , where g(−1)=−4 g(-1)=-4 and g(4)=1 g(4)=1 .\newlineWhich of the following is guaranteed by the Intermediate Value Theorem?\newlineChoose 11 answer:\newline(A) g(c)=−3 g(c)=-3 for at least one c c between −1-1 and 44\newline(B) g(c)=3 g(c)=3 for at least one c c between −4-4 and 11\newline(C) g(c)=−3 g(c)=-3 for at least one c c between −4-4 and 11\newline(D) g(c)=3 g(c)=3 for at least one c c between −1-1 and 44
Get tutor helpright-arrow

Posted 8 months ago

View all (89)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant