Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Joe is taking out a loan for
$1,500 with an annual compound interest rate of
15% for 3 years. Joe will not make any additional deposits or withdrawals. What will be the total balance paid at the end of 3 years?

Joe is taking out a loan for $\$ 1,500$ with an annual compound interest rate of $15 \%$ for $3$ years. Joe will not make any additional deposits or withdrawals. What will be the total balance paid at the end of $3$ years?

View step-by-step help

View step-by-step help

Finance problems

Full solution

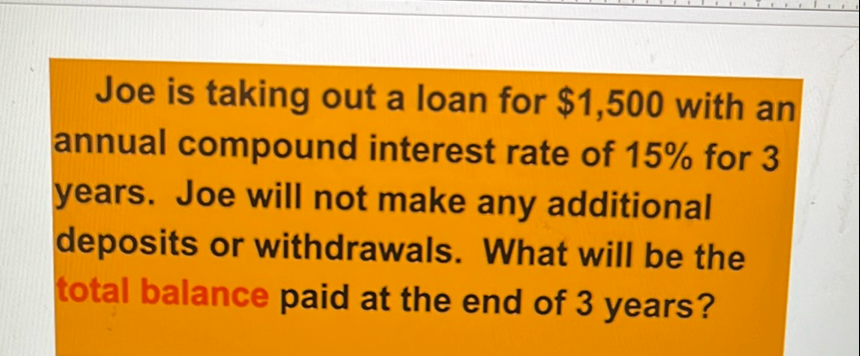
Q. Joe is taking out a loan for

\$ 1,500

with an annual compound interest rate of

15 \%

for

3

years. Joe will not make any additional deposits or withdrawals. What will be the total balance paid at the end of

3

years?

Identify Variables: Identify the variables for the compound interest formula. $\newline$ Principal amount $P$ = $\$1,500$ $\newline$ Annual interest rate $r$ = $15\%$ or $0.15$ (as a decimal) $\newline$ Number of years $t$ = $3$ $\newline$ Compound frequency $n$ = $1$ (since no specific compounding frequency is mentioned, we assume it is compounded annually)
Use Formula: Use the compound interest formula to calculate the total balance at the end of $3$ years. $\newline$ The compound interest formula is $A = P(1 + r/n)^{(nt)}$ , where $A$ is the amount of money accumulated after $n$ years, including interest. $\newline$ Substitute the given values into the formula: $\newline$ $A = 1500(1 + 0.15/1)^{(1*3)}$
Calculate Total Balance: Calculate the total balance using the formula. $\newline$ $A = 1500(1 + 0.15)^{3}$ $\newline$ $A = 1500(1.15)^{3}$ $\newline$ $A = 1500 \times 1.15^3$ $\newline$ $A = 1500 \times 1.520875$ $\newline$ $A = 2281.3125$
Check Calculation: Check the calculation for any mathematical errors. $\newline$ Re-evaluate the exponent: $\newline$ $1.15^3 = 1.520875$ (correct) $\newline$ Multiply by the principal amount: $\newline$ $1500 \times 1.520875 = 2281.3125$ (correct)

More problems from Finance problems

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago