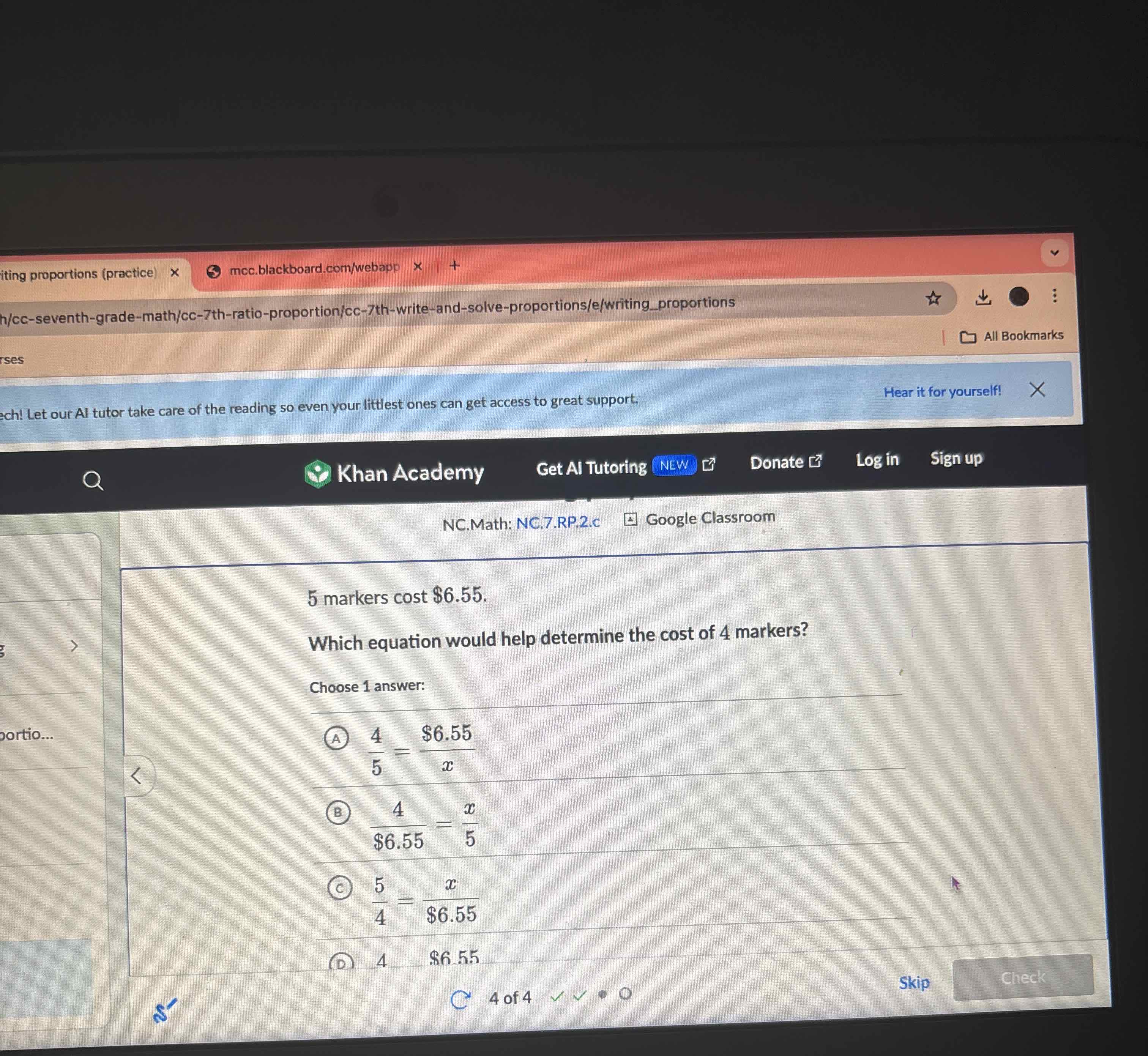
5 markers cost $6.55. Which equation would help determine the cost of 4 markers? Choose 1 answer: (A) (4)/(5)=($6.55)/(x) (B) (4)/($6.55)=(x)/(5) (C) (5)/(4)=(x)/($6.55) (D) 4quad$6.55

Question

5 markers cost  $6.55. Which equation would help determine the cost of 4 markers? Choose 1 answer: (A)  (4)/(5)=($6.55)/(x) (B)  (4)/($6.55)=(x)/(5) (C)  (5)/(4)=(x)/($6.55) (D)  4quad$6.55

Bytelearn · Accepted Answer

Understand the problem:  Step 1: Understand the problem. We need to find the cost of 4 markers based on the cost of 5 markers. We set up a proportion where one side represents the number of markers and the other side represents the cost. Set up the proportion:  Step 2: Set up the proportion. Since 5 markers cost $6.55, we can say that the cost per marker is constant. Therefore, the ratio of the number of markers to the cost should be the same for 4 markers. The correct setup is (number of markers)/(cost) = (number of markers)/(cost). Analyze the options:  Step 3: Analyze the options.  Option (A) (4/5) = ($6.55/x) correctly sets up the proportion where the number of markers is directly proportional to the cost.  Option (B) (4/$6.55) = (x/5) incorrectly sets up the proportion, mixing costs and number of markers on different sides. Option (C) (5/4) = (x/$6.55) also incorrectly sets up the proportion, reversing the relationship. Option (D) 4quad$6.55 is not a proportion but just a multiplication, which doesn't help in finding the cost per marker.

$5$ markers cost $\$6.55$ . Which equation would help determine the cost of $4$ markers? Choose $1$ answer: $\newline$ (A) $\frac{4}{5}=\frac{\$6.55}{x}$ $\newline$ (B) $\frac{4}{\$6.55}=\frac{x}{5}$ $\newline$ (C) $\frac{5}{4}=\frac{x}{\$6.55}$ $\newline$ (D) $4\quad\$6.55$

Full solution

More problems from One-step inequalities: word problems

Related topics