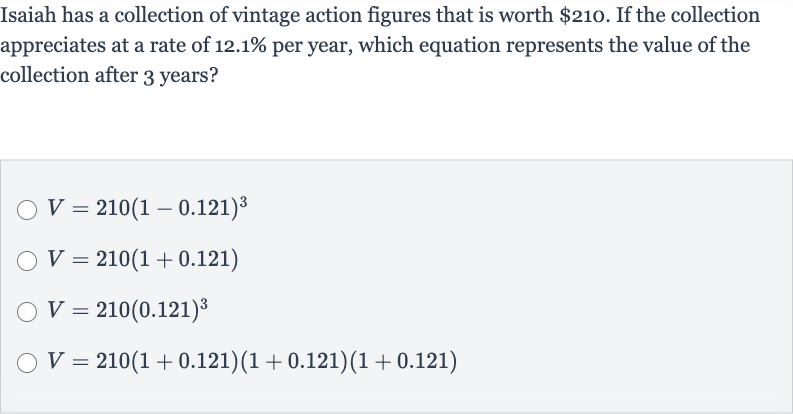Isaiah has a collection of vintage action figures that is worth $\$ 210$ . If the collection appreciates at a rate of $12.1 \%$ per year, which equation represents the value of the collection after $3$ years? $\newline$ $V=210(1-0.121)^{3}$ $\newline$ $V=210(1+0.121)$ $\newline$ $V=210(0.121)^{3}$ $\newline$ $V=210(1+0.121)(1+0.121)(1+0.121)$

View step-by-step help

Home

Math Problems

Algebra 2

Exponential growth and decay: word problems

Full solution

Q. Isaiah has a collection of vintage action figures that is worth

\$ 210

. If the collection appreciates at a rate of

12.1 \%

per year, which equation represents the value of the collection after

3

years?

\newline

V=210(1-0.121)^{3}

\newline

V=210(1+0.121)

\newline

V=210(0.121)^{3}

\newline

V=210(1+0.121)(1+0.121)(1+0.121)

Identify Values: We need to find the equation that correctly calculates the value of the collection after $3$ years with an appreciation rate of $12.1\%$ per year. The general formula for compound interest (which is similar to appreciation) is $V = P(1 + r)^t$ , where $V$ is the future value, $P$ is the initial principal balance, $r$ is the rate of interest per period, and $t$ is the number of periods.
Substitute Values: Let's identify the values from the problem: $\newline$ Initial value $P$ = $\$210$ $\newline$ Annual appreciation rate $r$ = $12.1\%$ = $0.121$ (as a decimal) $\newline$ Number of years $t$ = $3$ $\newline$ Now we can substitute these values into the formula.
Check Given Options: Substitute the values into the formula: $V = P(1 + r)^t$ $V = 210(1 + 0.121)^3$ This equation represents the value of the collection after $3$ years, taking into account the annual appreciation.
Final Equation: Now let's check the given options to see which one matches our equation: $\newline$ $V=210(1-0.121)^{3}$ - This is incorrect because it subtracts the rate instead of adding it. $\newline$ $V=210(1+0.121)$ - This is incorrect because it does not account for compounding over $3$ years. $\newline$ $V=210(0.121)^{3}$ - This is incorrect because it only raises the rate to the power of $3$ , not the entire term $(1 + \text{rate})$ . $\newline$ $V=210(1+0.121)(1+0.121)(1+0.121)$ - This is the expanded form of our correct equation and is equivalent to $V = 210(1 + 0.121)^3$ .