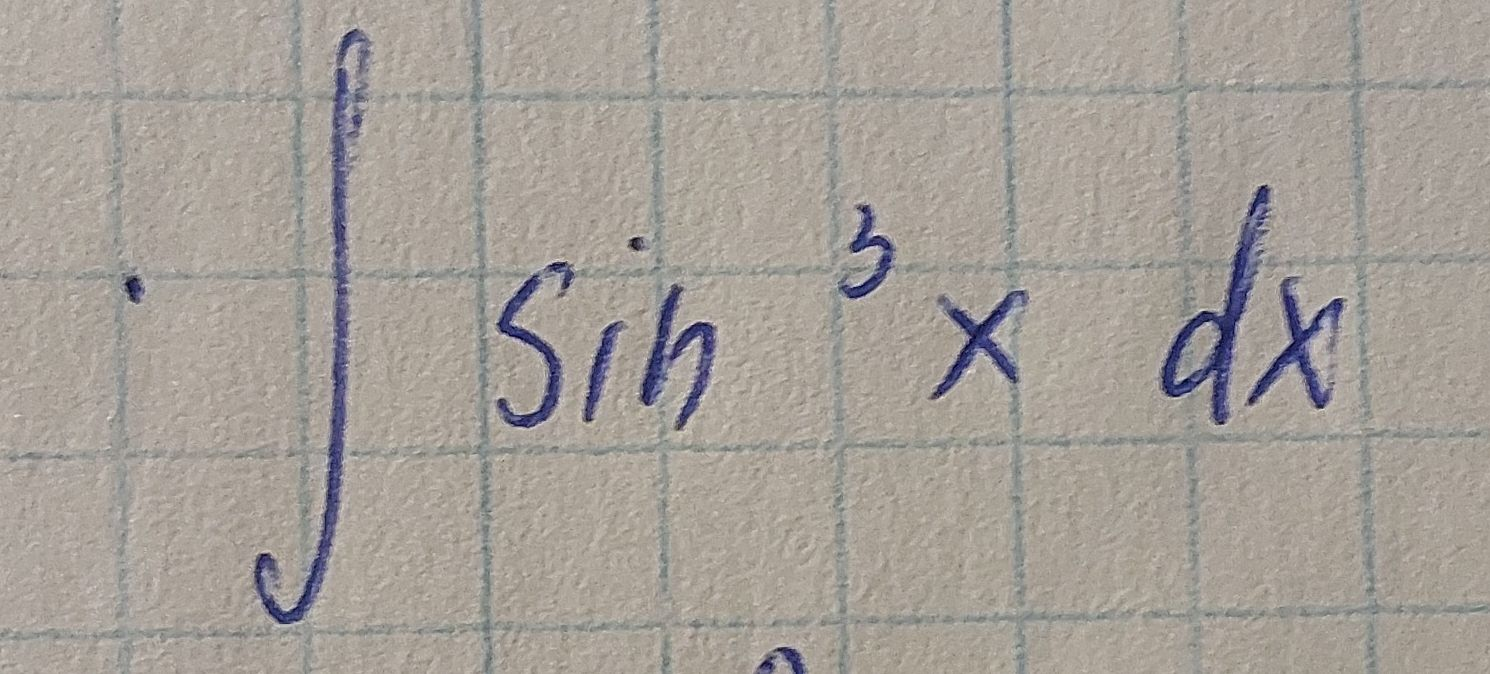Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

intsin^(3)xdx=

$\int \sin ^{3} x d x$ =

View step-by-step help

View step-by-step help

Power property of logarithms

Full solution

Q.

\int \sin ^{3} x d x

=

Recognize Problem: Recognize the integral that needs to be solved. $\newline$ We need to integrate $\sin^3(x)$ with respect to $x$ .
Use Identity: Use the identity $\sin^2(x) = 1 - \cos^2(x)$ to rewrite $\sin^3(x)$ as $\sin(x) \cdot \sin^2(x)$ . $\newline$ $\sin^3(x) = \sin(x) \cdot (1 - \cos^2(x))$
Substitute and Split: Substitute $\sin^2(x)$ in the integral. $\newline$ $\int \sin^3(x)\,dx = \int \sin(x) \cdot (1 - \cos^2(x))\,dx$
Integrate $\sin(x)$ : Split the integral into two separate integrals. $\newline$ \int\sin(x) \cdot (\(1 - \cos^ $2$ (x))\,dx = \int\sin(x)\,dx - \int\sin(x)\cos^ $2$ (x)\,dx
Use Substitution: Integrate the first part $\int \sin(x)\,dx$ . The integral of $\sin(x)$ with respect to $x$ is $-\cos(x)$ . So, $\int \sin(x)\,dx = -\cos(x)$
Integrate $u^2$ : Use substitution to integrate the second part $\int \sin(x)\cos^2(x)\,dx$ . Let $u = \cos(x)$ , then $du = -\sin(x)\,dx$ . Rewrite the integral: $-\int u^2\,du$
Substitute back: Integrate $-\int u^2\,du$ . $\newline$ The integral of $u^2$ with respect to $u$ is $(1/3)u^3$ . $\newline$ So, $-\int u^2\,du = -(1/3)u^3$
Combine Results: Substitute back $\cos(x)$ for $u$ . $\newline$ $-\frac{1}{3}u^3$ becomes $-\frac{1}{3}\cos^3(x)$ .
Combine Results: Substitute back $\cos(x)$ for $u$ . $-\frac{1}{3}u^3$ becomes $-\frac{1}{3}\cos^3(x)$ .Combine the results from Step $5$ and Step $8$ . The final answer is the sum of the two integrals: $-\cos(x) - \frac{1}{3}\cos^3(x) + C$ , where $C$ is the constant of integration.

More problems from Power property of logarithms

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 1 month ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago