AI tutor
Full solution
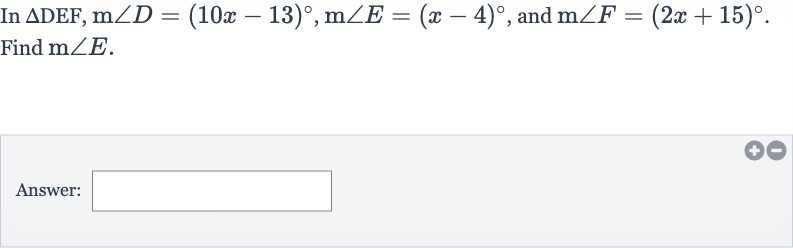
Q. In , and . Find .Answer:
- Recognize Triangle Angle Sum: Recognize that the sum of the angles in any triangle is degrees.Using the angle sum property of triangles: degrees
- Substitute Given Expressions: Substitute the given expressions for , , and into the angle sum equation.
- Combine Like Terms: Combine like terms on the left side of the equation.
- Add to Isolate Terms: Add to both sides of the equation to isolate the terms with on one side.
- Divide to Solve for x: Divide both sides of the equation by to solve for x.
- Substitute Value of : Substitute the value of back into the expression for to find the measure of angle E. degrees degrees degrees
More problems from Solve multi-step equations with fractional coefficients
QuestionGet tutor help