Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

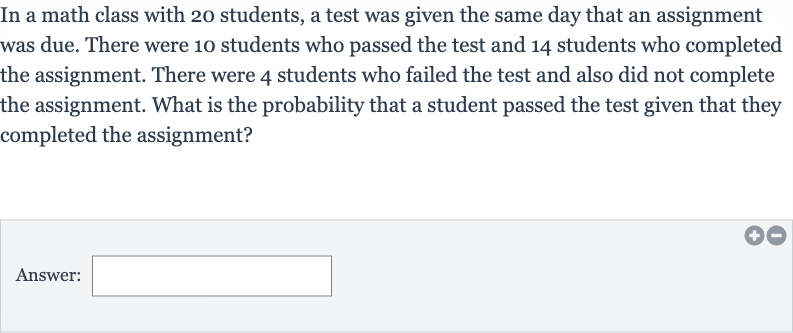
In a math class with 20 students, a test was given the same day that an assignment was due. There were 10 students who passed the test and 14 students who completed the assignment. There were 4 students who failed the test and also did not complete the assignment. What is the probability that a student passed the test given that they completed the assignment? Answer:

In a math class with 2020 students, a test was given the same day that an assignment was due. There were 1010 students who passed the test and 1414 students who completed the assignment. There were 44 students who failed the test and also did not complete the assignment. What is the probability that a student passed the test given that they completed the assignment?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 8right chevron icon
Probability of independent and dependent eventsright chevron icon

Full solution

Q. In a math class with 2020 students, a test was given the same day that an assignment was due. There were 1010 students who passed the test and 1414 students who completed the assignment. There were 44 students who failed the test and also did not complete the assignment. What is the probability that a student passed the test given that they completed the assignment?\newlineAnswer:
  1. Identify Total Students: First, let's identify the total number of students who completed the assignment, which is given as 1414 students.
  2. Find Passing Students: Next, we need to find out how many students passed the test among those who completed the assignment. We know that 1010 students passed the test in total, and 44 students both failed the test and did not complete the assignment. This means that the number of students who passed the test but did not complete the assignment is the total number of students who passed the test minus the number of students who passed the test and completed the assignment.
  3. Calculate Students Passed: Since there are 2020 students in total and 44 students neither passed the test nor completed the assignment, the number of students who either passed the test or completed the assignment (or both) is 20−4=1620 - 4 = 16 students.
  4. Determine Probability: Now, we know that 1414 students completed the assignment. Since 1616 students either passed the test or completed the assignment, and 1010 students passed the test, we can use the principle of inclusion-exclusion to find the number of students who both passed the test and completed the assignment: 10+14−16=810 + 14 - 16 = 8 students.
  5. Calculate Probability: The probability that a student passed the test given that they completed the assignment is the number of students who both passed the test and completed the assignment divided by the total number of students who completed the assignment. So, the probability is 814\frac{8}{14}.
  6. Simplify Fraction: To simplify the fraction, we divide both the numerator and the denominator by their greatest common divisor, which is 22. So, 814\frac{8}{14} simplifies to 47\frac{4}{7}.

More problems from Probability of independent and dependent events

Question
You roll a 66-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage. \newline____ `%`
Get tutor helpright-arrow

Posted 5 months ago

Question
There are 99 college students running for student government class president. The candidates include 77 education majors.\newlineIf 66 of the candidates are randomly chosen to give the first 66 speeches, what is the probability that all of them are education majors?\newlineWrite your answer as a decimal rounded to four decimal places.
Get tutor helpright-arrow

Posted 8 months ago

Question
In an experiment, the probability that event A A occurs is 27 \frac{2}{7} , the probability that event B B occurs is 79 \frac{7}{9} , and the probability that events A A and B B both occur is 19 \frac{1}{9} .\newlineAre A A and B B independent events?\newlineChoices:\newline(A) yes\text{yes}\newline(B) no\text{no}
Get tutor helpright-arrow

Posted 8 months ago

Question
At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.\newlineThe probability that a competitor reacted in over 0.70.7 seconds is 0.60.6, the probability that a competitor was female is 0.40.4, and the probability that a competitor reacted in over 0.70.7 seconds and was female is 0.30.3.\newlineWhat is the probability that a randomly chosen competitor reacted in over 0.70.7 seconds or was female?\newlineWrite your answer as a whole number, decimal, or simplified fraction.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 8 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 8 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 8 months ago

View all (56)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant