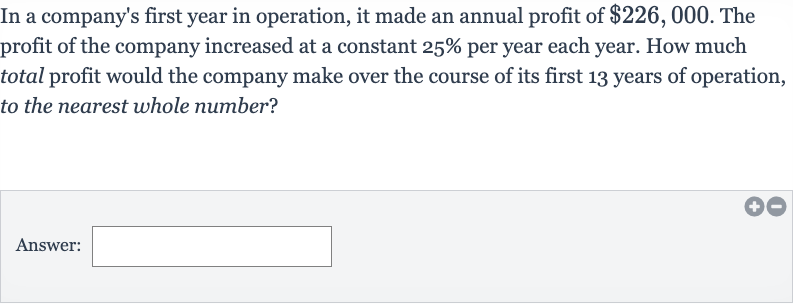
In a company's first year in operation, it made an annual profit of $226,000. The profit of the company increased at a constant 25% per year each year. How much total profit would the company make over the course of its first 13 years of operation, to the nearest whole number? Answer:

Question

In a company's first year in operation, it made an annual profit of  $226,000. The profit of the company increased at a constant  25% per year each year. How much total profit would the company make over the course of its first 13 years of operation, to the nearest whole number? Answer:

Bytelearn · Accepted Answer

Identify initial profit and rate: Identify the initial profit and the rate of increase. The initial profit is $226,000, and the profit increases by 25% each year.Determine formula for total profit: Determine the formula to calculate the total profit over 13 years. The profit follows a geometric sequence where each term is 1.25 times the previous term (since the profit increases by 25% each year). The formula for the sum of a geometric series is S_n = a(1 - r^n) / (1 - r), where: - S_n is the sum of the first n terms, - a is the first term, - r is the common ratio, - n is the number of terms. Here, a = $226,000, r = 1.25, and n = 13.Calculate total profit formula: Calculate the total profit using the geometric series sum formula. S_13 = 226,000(1 - 1.25^13) / (1 - 1.25)Perform necessary calculations: Perform the calculations. First, calculate 1.25^13: 1.25^13 ≈ 18.14 (rounded to two decimal places for simplicity) Then, substitute this value into the formula: S_13 = 226,000(1 - 18.14) / (1 - 1.25) S_13 = 226,000(-17.14) / (-0.25)Continue calculation: Continue the calculation. S_13 = 226,000 * 17.14 / 0.25 S_13 = 3,874,040 / 0.25 S_13 = 15,496,160Round total profit: Round the total profit to the nearest whole number. The total profit to the nearest whole number is $15,496,160.

Full solution

More problems from Exponential growth and decay: word problems

Related topics