Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

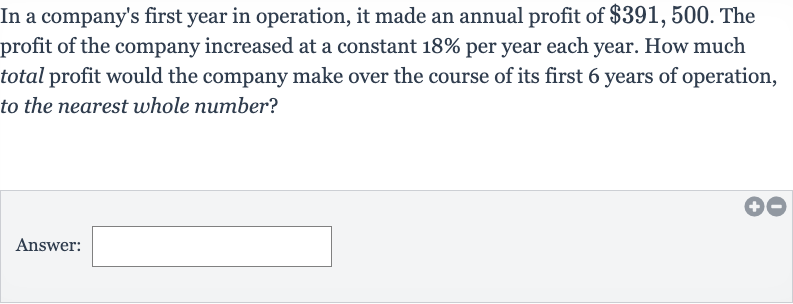
In a company's first year in operation, it made an annual profit of
$391,500. The profit of the company increased at a constant
18% per year each year. How much total profit would the company make over the course of its first 6 years of operation, to the nearest whole number?
Answer:

In a company's first year in operation, it made an annual profit of $\$ 391,500$ . The profit of the company increased at a constant $18 \%$ per year each year. How much total profit would the company make over the course of its first $6$ years of operation, to the nearest whole number? $\newline$ Answer:

View step-by-step help

View step-by-step help

Exponential growth and decay: word problems

Full solution

Q. In a company's first year in operation, it made an annual profit of

\$ 391,500

. The profit of the company increased at a constant

18 \%

per year each year. How much total profit would the company make over the course of its first

6

years of operation, to the nearest whole number?

\newline

Answer:

Identify Initial Profit: Identify the initial profit and the annual increase rate. $\newline$ The initial profit is $\$391,500$ , and the profit increases by $18\%$ each year.
Calculate Yearly Profits: Calculate the profit for each year using the formula for compound interest: $P = P_0 \times (1 + r)^n$ , where $P_0$ is the initial amount, $r$ is the rate of increase, and $n$ is the number of years. $\newline$ Year $1$ : $P = \$391,500$ $\newline$ Year $2$ : $P = \$391,500 \times (1 + 0.18)^1$ $\newline$ Year $3$ : $P = \$391,500 \times (1 + 0.18)^2$ $\newline$ Year $4$ : $P = \$391,500 \times (1 + 0.18)^3$ $\newline$ Year $5$ : $P = \$391,500 \times (1 + 0.18)^4$ $\newline$ Year $6$ : $P = \$391,500 \times (1 + 0.18)^5$
Calculate Individual Profits: Calculate the profit for each year. $\newline$ Year $2$ : $P = \$391,500 \times 1.18 = \$462,170$ $\newline$ Year $3$ : $P = \$391,500 \times (1.18)^2 = \$545,360.60$ $\newline$ Year $4$ : $P = \$391,500 \times (1.18)^3 = \$643,525.51$ $\newline$ Year $5$ : $P = \$391,500 \times (1.18)^4 = \$759,360.50$ $\newline$ Year $6$ : $P = \$391,500 \times (1.18)^5 = \$896,045.39$
Calculate Total Profit: Add up the profits for each year to get the total profit over $6$ years. $\newline$ Total Profit = Year $1$ + Year $2$ + Year $3$ + Year $4$ + Year $5$ + Year $6$ $\newline$ Total Profit = $\$391,500$ + $\$462,170$ + $\$545,360.60$ + $\$643,525.51$ + $\$759,360.50$ + $\$896,045.39$
Perform Addition: Perform the addition to find the total profit. $\newline$ Total Profit = $\$391,500 + \$462,170 + \$545,360.60 + \$643,525.51 + \$759,360.50 + \$896,045.39 = \$3,697,962$

More problems from Exponential growth and decay: word problems

Question

Use the following function rule to find

f(2)

\newline

f(x) = 11 \cdot (9)^x + 8

\newline

f(2) =

Posted 5 months ago

Question

Raymond works for a pharmaceutical company that is testing the effectiveness of a new medication. He gave one of the study participants

400

milligrams of the medication, and he knows the amount remaining in the participant's body will decrease by a factor of

1/3

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the amount of medication,

y

, remaining in the participant's body after

x

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

\newline

Posted 8 months ago

Question

100

bacteria doubles in size every

60

hours. What will the population be

180

?

Posted 4 months ago

Question

Charlotte opened a savings account and deposited

\$800.00

as principal. The account earns

8\%

interest, compounded annually. What is the balance after

10

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

Posted 4 months ago

Question

Bob rented a car for a flat fee of `$150` and an additional `$10` per day. Write a linear function that represents the total cost,

f(x)

x

Posted 10 months ago

Question

Sally purchased a laptop for `$800` and has to pay a service fee of `$20` for each day until it is delivered. Write a linear function to represent the total cost,

h(x)

x

Posted 10 months ago

Question

\$1,000

in a savings account with a daily interest rate of

0.1\%

. Write an exponential function to represent the total amount,

s(x)

, in his account after

x

Posted 9 months ago

Question

A=2450+740 s

\newline

The total amount,

A

, in thousands of dollars, of scholarship money given out by a college throughout its history at a time of

s

semesters after the summer of the year

2000

is given by the equation. What was the total amount of scholarship money, in thousands of dollars, given out by the college up to the summer of the year

2000

Posted 5 months ago

Question

T=235+980 d

\newline

T

, in newton-meters, on a diving board with a

100

kilogram weight placed

d

meters from the diving board's fulcrum is given by the equation. How much torque in newton-meters is on the diving board when the weight is placed at the fulcrum?

Posted 8 months ago

Question

R=42-0.7 t

\newline

Quinn returned home one summer's day to find it extremely hot. He turned the air conditioner on, and the room's temperature began decreasing at a constant rate. The given equation shown gives the room's temperature,

R

, in degrees Celsius,

t

minutes after Quinn turned on the air conditioner. What was the room's temperature, in degrees Celsius, when Quinn returned home?

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant