Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

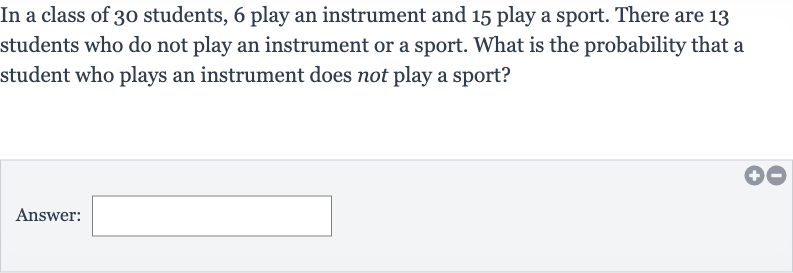
In a class of 30 students, 6 play an instrument and 15 play a sport. There are 13 students who do not play an instrument or a sport. What is the probability that a student who plays an instrument does not play a sport? Answer:

In a class of 3030 students, 66 play an instrument and 1515 play a sport. There are 1313 students who do not play an instrument or a sport. What is the probability that a student who plays an instrument does not play a sport?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 8right chevron icon
Probability of independent and dependent eventsright chevron icon

Full solution

Q. In a class of 3030 students, 66 play an instrument and 1515 play a sport. There are 1313 students who do not play an instrument or a sport. What is the probability that a student who plays an instrument does not play a sport?\newlineAnswer:
  1. Determine Number of Students: Let's first determine the number of students who play only an instrument. We know that there are 66 students who play an instrument and 1313 students who do not play an instrument or a sport. Since there are 3030 students in total, we can find the number of students who play both an instrument and a sport by subtracting the number of students who play only an instrument and those who do not play anything from the total number of students.\newlineTotal number of students = Number of students who play only an instrument + Number of students who play both an instrument and a sport + Number of students who do not play anything\newline30=6+(Number of students who play both an instrument and a sport)+1330 = 6 + (\text{Number of students who play both an instrument and a sport}) + 13
  2. Solve for Both Instrument and Sport: Now, let's solve for the number of students who play both an instrument and a sport.\newline30=6+(Number of students who play both an instrument and a sport)+1330 = 6 + (\text{Number of students who play both an instrument and a sport}) + 13\newline30=19+(Number of students who play both an instrument and a sport)30 = 19 + (\text{Number of students who play both an instrument and a sport})\newline(Number of students who play both an instrument and a sport)=30−19(\text{Number of students who play both an instrument and a sport}) = 30 - 19\newline(Number of students who play both an instrument and a sport)=11(\text{Number of students who play both an instrument and a sport}) = 11
  3. Find Students Playing Only Instrument: Next, we need to find the number of students who play only an instrument. This can be found by subtracting the number of students who play both an instrument and a sport from the total number of students who play an instrument.\newlineNumber of students who play only an instrument == Total number of students who play an instrument −- Number of students who play both an instrument and a sport\newlineNumber of students who play only an instrument =6−11= 6 - 11
  4. Correct Error: Let's correct the error from the previous step. We need to find the number of students who play only an instrument, which is the total number of students who play an instrument minus the number of students who play both an instrument and a sport.\newlineNumber of students who play only an instrument == Total number of students who play an instrument −- Number of students who play both an instrument and a sport\newlineNumber of students who play only an instrument =6−(= 6 - (Number of students who play both an instrument and a sport))\newlineSince we have not yet determined the number of students who play both an instrument and a sport, we cannot complete this calculation yet. We need to find this number first.
  5. Find Students Playing Both Instrument and Sport: Let's find the number of students who play both an instrument and a sport. We know that there are 1515 students who play a sport and 1313 students who do not play an instrument or a sport. Therefore, the number of students who play a sport and possibly an instrument is:\newlineNumber of students who play a sport and possibly an instrument = Total number of students - Number of students who do not play an instrument or a sport\newlineNumber of students who play a sport and possibly an instrument = 30−1330 - 13\newlineNumber of students who play a sport and possibly an instrument = 1717
  6. Find Students Playing Only Sport: Now, we can find the number of students who play both an instrument and a sport by subtracting the number of students who play only a sport from the number of students who play a sport and possibly an instrument.\newlineNumber of students who play both an instrument and a sport == Number of students who play a sport and possibly an instrument −- Number of students who play only a sport\newlineSince we know that 1515 students play a sport, we can assume that the remaining 22 students (from the 1717 calculated in the previous step) must be the ones who play both an instrument and a sport.\newlineNumber of students who play both an instrument and a sport =17−15= 17 - 15\newlineNumber of students who play both an instrument and a sport =2= 2
  7. Calculate Probability: Now that we have the number of students who play both an instrument and a sport, we can find the number of students who play only an instrument.\newlineNumber of students who play only an instrument == Total number of students who play an instrument −- Number of students who play both an instrument and a sport\newlineNumber of students who play only an instrument =6−2= 6 - 2\newlineNumber of students who play only an instrument =4= 4
  8. Calculate Probability: Now that we have the number of students who play both an instrument and a sport, we can find the number of students who play only an instrument.\newlineNumber of students who play only an instrument == Total number of students who play an instrument −- Number of students who play both an instrument and a sport\newlineNumber of students who play only an instrument =6−2= 6 - 2\newlineNumber of students who play only an instrument =4= 4Finally, we can calculate the probability that a student who plays an instrument does not play a sport. This is the number of students who play only an instrument divided by the total number of students who play an instrument.\newlineProbability == Number of students who play only an instrument / Total number of students who play an instrument\newlineProbability == 46\frac{4}{6}\newlineProbability == 23\frac{2}{3}

More problems from Probability of independent and dependent events

Question
You roll a 66-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage. \newline____ `%`
Get tutor helpright-arrow

Posted 5 months ago

Question
There are 99 college students running for student government class president. The candidates include 77 education majors.\newlineIf 66 of the candidates are randomly chosen to give the first 66 speeches, what is the probability that all of them are education majors?\newlineWrite your answer as a decimal rounded to four decimal places.
Get tutor helpright-arrow

Posted 8 months ago

Question
In an experiment, the probability that event A A occurs is 27 \frac{2}{7} , the probability that event B B occurs is 79 \frac{7}{9} , and the probability that events A A and B B both occur is 19 \frac{1}{9} .\newlineAre A A and B B independent events?\newlineChoices:\newline(A) yes\text{yes}\newline(B) no\text{no}
Get tutor helpright-arrow

Posted 8 months ago

Question
At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.\newlineThe probability that a competitor reacted in over 0.70.7 seconds is 0.60.6, the probability that a competitor was female is 0.40.4, and the probability that a competitor reacted in over 0.70.7 seconds and was female is 0.30.3.\newlineWhat is the probability that a randomly chosen competitor reacted in over 0.70.7 seconds or was female?\newlineWrite your answer as a whole number, decimal, or simplified fraction.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 8 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 8 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 8 months ago

View all (56)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant