Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

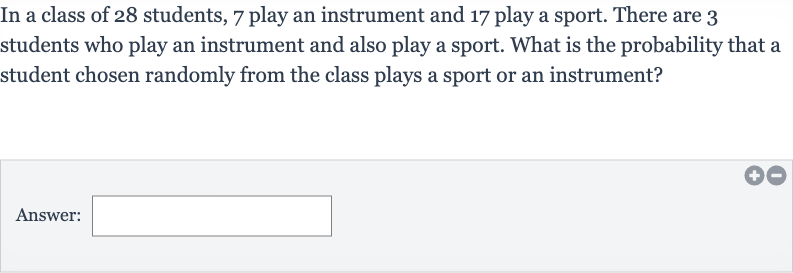
In a class of 28 students, 7 play an instrument and 17 play a sport. There are 3 students who play an instrument and also play a sport. What is the probability that a student chosen randomly from the class plays a sport or an instrument?
Answer:

In a class of $28$ students, $7$ play an instrument and $17$ play a sport. There are $3$ students who play an instrument and also play a sport. What is the probability that a student chosen randomly from the class plays a sport or an instrument? $\newline$ Answer:

View step-by-step help

View step-by-step help

Probability of independent and dependent events

Full solution

Q. In a class of

28

students,

7

play an instrument and

17

play a sport. There are

3

students who play an instrument and also play a sport. What is the probability that a student chosen randomly from the class plays a sport or an instrument?

\newline

Answer:

Calculate Total Students: Determine the total number of students who play either a sport or an instrument, or both. $\newline$ To find the number of students who play either a sport or an instrument, we add the number of students who play an instrument to the number of students who play a sport. However, we must subtract the number of students who do both to avoid double-counting. $\newline$ Number of students who play either a sport or an instrument = Number of students who play an instrument $+$ Number of students who play a sport $-$ Number of students who do both $\newline$ Calculation: $7$ (instrument players) $+ 17$ (sport players) $- 3$ (both) $= 21$
Calculate Probability: Calculate the probability that a student chosen randomly from the class plays a sport or an instrument. $\newline$ The probability is the number of students who play either a sport or an instrument divided by the total number of students in the class. $\newline$ Probability = $\frac{\text{Number of students who play either a sport or an instrument}}{\text{Total number of students}}$ $\newline$ Calculation: $\frac{21}{28}$
Simplify Fraction: Simplify the fraction obtained in Step $2$ to get the final probability. $\newline$ Calculation: $21 / 28$ can be simplified by dividing both the numerator and the denominator by $7$ . $\newline$ $21 \div 7 = 3$ $\newline$ $28 \div 7 = 4$ $\newline$ So, the simplified fraction is $3/4$ .

More problems from Probability of independent and dependent events

Question

6

-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage.

\newline

Posted 5 months ago

Question

9

college students running for student government class president. The candidates include

7

education majors.

\newline

6

of the candidates are randomly chosen to give the first

6

speeches, what is the probability that all of them are education majors?

\newline

Write your answer as a decimal rounded to four decimal places.

Posted 8 months ago

Question

In an experiment, the probability that event

A

\frac{2}{7}

, the probability that event

B

\frac{7}{9}

, and the probability that events

A

B

\frac{1}{9}

\newline

A

B

independent events?

\newline

\newline

\text{yes}

\newline

\text{no}

Posted 8 months ago

Question

At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.

\newline

The probability that a competitor reacted in over

0.7

0.6

, the probability that a competitor was female is

0.4

, and the probability that a competitor reacted in over

0.7

seconds and was female is

0.3

\newline

What is the probability that a randomly chosen competitor reacted in over

0.7

seconds or was female?

\newline

Write your answer as a whole number, decimal, or simplified fraction.

\newline

Posted 8 months ago

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 7 months ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 8 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 8 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 8 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 8 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant