Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

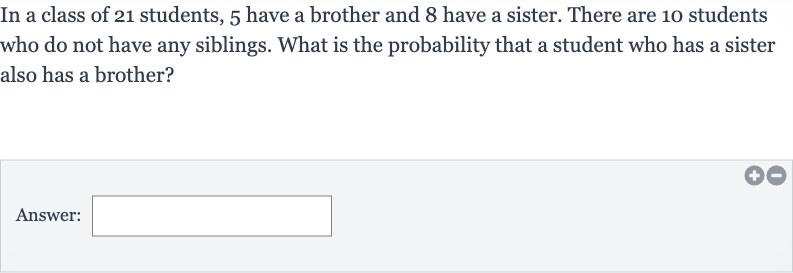
In a class of 21 students, 5 have a brother and 8 have a sister. There are 10 students who do not have any siblings. What is the probability that a student who has a sister also has a brother? Answer:

In a class of 2121 students, 55 have a brother and 88 have a sister. There are 1010 students who do not have any siblings. What is the probability that a student who has a sister also has a brother?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find probabilities using the binomial distributionright chevron icon

Full solution

Q. In a class of 2121 students, 55 have a brother and 88 have a sister. There are 1010 students who do not have any siblings. What is the probability that a student who has a sister also has a brother?\newlineAnswer:
  1. Determine Siblings Count: First, we need to determine the number of students who have both a brother and a sister. Since there are 1010 students without any siblings, the remaining students must have at least one sibling. We subtract the number of students without siblings from the total number of students to find the number of students with siblings.\newline2121 students - 1010 students without siblings = 1111 students with siblings.
  2. Find Overlap: Next, we know that 55 students have a brother and 88 have a sister. However, this does not tell us directly how many have both, as some students could be counted in both groups. We need to find the overlap between the two groups.\newlineSince there are 1111 students with siblings and more than 1111 students if we add those with a brother and those with a sister (5+8=135 + 8 = 13), there must be an overlap.
  3. Calculate Probability: To find the overlap, we can use the principle of inclusion-exclusion. We add the number of students with a brother and the number of students with a sister, then subtract the total number of students with siblings.\newlineOverlap (students with both a brother and a sister) = (students with a brother) + (students with a sister) - (students with siblings)\newlineOverlap =5+8−11=2= 5 + 8 - 11 = 2 students.
  4. Simplify Fraction: Now, we can calculate the probability that a student who has a sister also has a brother. This is the number of students with both a brother and a sister divided by the number of students with a sister.\newlineProbability = Number of students with both a brother and a sisterNumber of students with a sister\frac{\text{Number of students with both a brother and a sister}}{\text{Number of students with a sister}}\newlineProbability = 28\frac{2}{8}
  5. Simplify Fraction: Now, we can calculate the probability that a student who has a sister also has a brother. This is the number of students with both a brother and a sister divided by the number of students with a sister.\newlineProbability = Number of students with both a brother and a sisterNumber of students with a sister\frac{\text{Number of students with both a brother and a sister}}{\text{Number of students with a sister}}\newlineProbability = 28\frac{2}{8}Finally, we simplify the fraction to get the probability.\newlineProbability = 28=14\frac{2}{8} = \frac{1}{4}

More problems from Find probabilities using the binomial distribution

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 9 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 9 months ago

Question
Y Y is the number of desserts available in a randomly chosen restaurant.\newlineIs the random variable Y Y discrete or continuous?\newlineChoices:\newline[A]discrete \text{[A]discrete} \newline[B]continuous \text{[B]continuous}
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous for all real numbers?\newlineg(x)=ln⁡(x) g(x)=\ln (x) \newlinef(x)=1x f(x)=\frac{1}{x} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newlineD Neither g g nor f f
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous at x=−1 x=-1 ?\newlineg(x)=sin⁡(x+1) g(x)=\sin (x+1) \newlinef(x)=1x−1 f(x)=\frac{1}{x-1} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newline(D) Neither g g nor f f
Get tutor helpright-arrow

Posted 8 months ago

Question
Let g g be a continuous function on the closed interval [−1,4] [-1,4] , where g(−1)=−4 g(-1)=-4 and g(4)=1 g(4)=1 .\newlineWhich of the following is guaranteed by the Intermediate Value Theorem?\newlineChoose 11 answer:\newline(A) g(c)=−3 g(c)=-3 for at least one c c between −1-1 and 44\newline(B) g(c)=3 g(c)=3 for at least one c c between −4-4 and 11\newline(C) g(c)=−3 g(c)=-3 for at least one c c between −4-4 and 11\newline(D) g(c)=3 g(c)=3 for at least one c c between −1-1 and 44
Get tutor helpright-arrow

Posted 8 months ago

View all (89)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant