Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

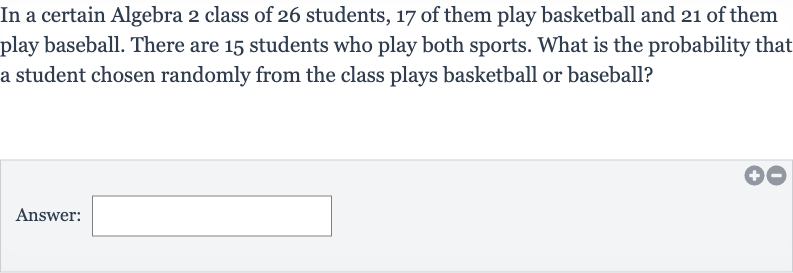
In a certain Algebra 2 class of 26 students, 17 of them play basketball and 21 of them play baseball. There are 15 students who play both sports. What is the probability that a student chosen randomly from the class plays basketball or baseball?
Answer:

In a certain Algebra $2$ class of $26$ students, $17$ of them play basketball and $21$ of them play baseball. There are $15$ students who play both sports. What is the probability that a student chosen randomly from the class plays basketball or baseball? $\newline$ Answer:

View step-by-step help

View step-by-step help

Probability of simple events

Full solution

Q. In a certain Algebra

2

class of

26

students,

17

of them play basketball and

21

of them play baseball. There are

15

students who play both sports. What is the probability that a student chosen randomly from the class plays basketball or baseball?

\newline

Answer:

Principle of Inclusion-Exclusion: To find the probability that a student chosen randomly from the class plays basketball or baseball, we need to use the principle of inclusion-exclusion. This principle states that for any two sets, the size of their union is the size of the first set plus the size of the second set minus the size of their intersection.
Given Information: First, let's identify the given information: $\newline$ - Total number of students in the class: $26$ $\newline$ - Number of students who play basketball: $17$ $\newline$ - Number of students who play baseball: $21$ $\newline$ - Number of students who play both sports: $15$
Calculate Students Playing Either Sport: Using the principle of inclusion-exclusion, we calculate the number of students who play either basketball or baseball (or both) as follows: $\newline$ Number of students who play basketball or baseball $=$ Number of students who play basketball $+$ Number of students who play baseball $-$ Number of students who play both sports
Plug in Numbers: Now, let's plug in the numbers: $\newline$ Number of students who play basketball or baseball = $17 + 21 - 15$
Perform Calculation: Perform the calculation: $\newline$ Number of students who play basketball or baseball = $38 - 15$
Continue Calculation: Continue the calculation: $\newline$ Number of students who play basketball or baseball = $23$
Calculate Probability: To find the probability, we divide the number of students who play basketball or baseball by the total number of students in the class: $\newline$ Probability = $\frac{\text{Number of students who play basketball or baseball}}{\text{Total number of students}}$
Express Probability: Now, let's calculate the probability: Probability = $\frac{23}{26}$
Express Probability: Now, let's calculate the probability: $\newline$ Probability = $\frac{23}{26}$ To express the probability in simplest form, we can leave it as a fraction or convert it to a decimal: $\newline$ Probability = $\frac{23}{26} \approx 0.8846$

More problems from Probability of simple events

Question

6

-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage. ____ `%`

Posted 1 month ago

Question

9

college students running for student government class president. The candidates include

7

education majors.

\newline

6

of the candidates are randomly chosen to give the first

6

speeches, what is the probability that all of them are education majors?

\newline

Write your answer as a decimal rounded to four decimal places.

Posted 2 months ago

Question

In an experiment, the probability that event

A

\frac{2}{7}

, the probability that event

B

\frac{7}{9}

, and the probability that events

A

B

\frac{1}{9}

\newline

A

B

independent events?

\newline

\newline

\text{yes}

\newline

\text{no}

Posted 2 months ago

Question

At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.

\newline

The probability that a competitor reacted in over

0.7

0.6

, the probability that a competitor was female is

0.4

, and the probability that a competitor reacted in over

0.7

seconds and was female is

0.3

\newline

What is the probability that a randomly chosen competitor reacted in over

0.7

seconds or was female?

\newline

Write your answer as a whole number, decimal, or simplified fraction.

\newline

Posted 2 months ago

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 1 month ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 2 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 2 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 2 months ago