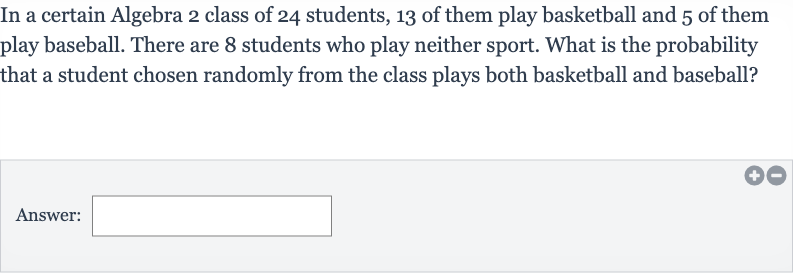
In a certain Algebra 2 class of 24 students, 13 of them play basketball and 5 of them play baseball. There are 8 students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball? Answer:

Question

Bytelearn · Accepted Answer

Define Variables: Let's denote the total number of students in the class as T, the number of students who play basketball as B, the number of students who play baseball as S, and the number of students who play neither sport as N. We are also looking for the number of students who play both sports, which we will denote as BS. We are given the following: T = 24 (total students) B = 13 (students playing basketball) S = 5 (students playing baseball) N = 8 (students playing neither sport) We need to find BS (students playing both sports).Find Students Playing Sports: First, let's find out how many students play at least one sport. Since there are 8 students who play neither sport, the number of students who play at least one sport is T - N. So, the number of students playing at least one sport is 24 - 8 = 16.Use Inclusion-Exclusion Principle: Now, let's use the principle of inclusion-exclusion to find the number of students who play both sports. The principle of inclusion-exclusion states that for any two sets, the number of elements in at least one of the sets is equal to the sum of the number of elements in each set minus the number of elements in both sets. So, the number of students playing both sports is B + S - (number of students playing at least one sport). We can calculate BS as 13 + 5 - 16 = 2.Calculate Probability: Now that we know there are 2 students who play both basketball and baseball, we can find the probability that a randomly chosen student from the class plays both sports. The probability is the number of students who play both sports divided by the total number of students. So, the probability is BS / T = 2 / 24.Simplify Fraction: Finally, we simplify the fraction 2 / 24 to its simplest form by dividing both the numerator and the denominator by their greatest common divisor, which is 2. So, the simplified probability is 1 / 12.

In a certain Algebra $2$ class of $24$ students, $13$ of them play basketball and $5$ of them play baseball. There are $8$ students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball? $\newline$ Answer:

Full solution

More problems from Find probabilities using the addition rule

Related topics

In a certain Algebra 222 class of 242424 students, 131313 of them play basketball and 555 of them play baseball. There are 888 students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball?\newlineAnswer:

In a certain Algebra $2$ class of $24$ students, $13$ of them play basketball and $5$ of them play baseball. There are $8$ students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball? $\newline$ Answer: