AI tutor
Full solution
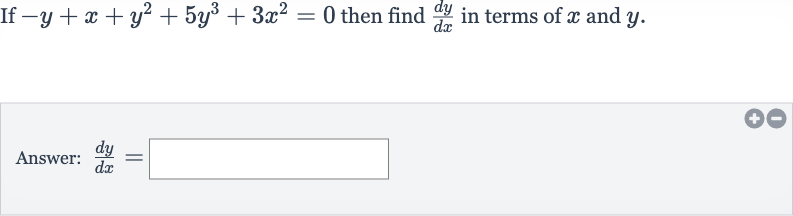
Q. If then find in terms of and .Answer:
- Given Equation: We are given the equation and we need to find the derivative of with respect to , which is . To do this, we will use implicit differentiation, which involves taking the derivative of both sides of the equation with respect to , while treating as a function of .
- Implicit Differentiation: First, we differentiate each term of the equation with respect to . For the terms involving only , we use the standard rules of differentiation. For the terms involving , we use the chain rule, remembering to multiply by since is a function of . The derivative of with respect to is . The derivative of with respect to is . The derivative of with respect to is . The derivative of with respect to is . The derivative of with respect to is .
- Differentiating Terms: Now we write down the differentiated equation:
- Writing Differentiated Equation: Next, we collect all the terms involving on one side and the terms not involving on the other side:\(-1\frac{dy}{dx} + y\frac{dy}{dx} + y^{}\frac{dy}{dx} = - x
- Solving for from the left side of the equation:(\frac{dy}{dx})(\(-1 + y + y^{}) = - x
- Solving for from the left side of the equation:Now we solve for by dividing both sides of the equation by