Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If
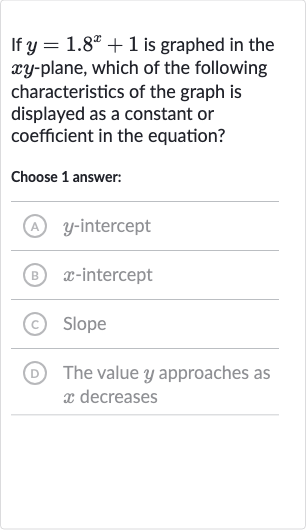
y=1.8^(x)+1 is graphed in the
xy-plane, which of the following characteristics of the graph is displayed as a constant or coefficient in the equation?
Choose 1 answer:
(A)
y-intercept
(B)
x-intercept
(C) Slope
(D) The value
y approaches as
x decreases

If $y=1.8^{x}+1$ is graphed in the $xy$ -plane, which of the following characteristics of the graph is displayed as a constant or coefficient in the equation? $\newline$ Choose $1$ answer: $\newline$ (A) $y$ -intercept $\newline$ (B) $x$ -intercept $\newline$ (C) Slope $\newline$ (D) The value $y$ approaches as $x$ decreases

View step-by-step help

View step-by-step help

Dilations of functions

Full solution

Q. If

y=1.8^{x}+1

is graphed in the

xy

-plane, which of the following characteristics of the graph is displayed as a constant or coefficient in the equation?

\newline

Choose

1

answer:

\newline

(A)

y

-intercept

\newline

(B)

x

-intercept

\newline

(C) Slope

\newline

(D) The value

y

approaches as

x

decreases

Identify constant term: Identify the constant term in the equation $y=1.8^{x}+1$ . $\newline$ The constant term in the equation is $+1$ . This term does not depend on the value of $x$ and is added to the value of $1.8^{x}$ for all $x$ .
Significance in graph: Determine the significance of the constant term in the context of the graph. $\newline$ The constant term in an exponential function like $y=1.8^{(x)}+1$ represents the vertical shift of the graph. In this case, the graph is shifted up by $1$ unit.
Relate to characteristics: Relate the constant term to the characteristics of the graph provided in the choices. $\newline$ The constant term affects the $y$ -intercept of the graph. The $y$ -intercept is the point where the graph crosses the $y$ -axis, which occurs when $x=0$ . Plugging $x=0$ into the equation $y=1.8^{(x)}+1$ gives $y=1.8^{(0)}+1$ , which simplifies to $y=1+1$ , or $y=2$ . This shows that the $y$ -intercept of the graph is $y$ $0$ , and it is directly given by the constant term $y$ $1$ in the equation.

More problems from Dilations of functions

Question

g(x)

g(x)

is the reflection across the x-axis of

f(x)=9|x+2|-4

\newline

\newline

\text{}(A)g(x) = 9|x+2| - 4\text{]}

\newline

\text{}(B)g(x) = 9|x-2| - 4\text{]}

\newline

\text{}(C)g(x)=-9|x-2| +4\text{]}

\newline

\text{(D)}g(x) = -9|x + 2| + 4\text{]}

Posted 2 months ago

Question

What does the transformation

f(x) \mapsto f(x - 4)

do to the graph of

f(x)

\newline

\newline

\text{translates it } 4 \text{ units right}

\newline

\text{translates it } 4 \text{ units down}

\newline

\text{translates it } 4 \text{ units left}

\newline

\text{translates it } 4 \text{ units up}

Posted 2 months ago

Question

What does the transformation

f(x) \mapsto f(4x)

do to the graph of

f(x)

\newline

\newline

[A] stretches it vertically

\newline

[B] stretches it horizontally

\newline

[C]shrinks it horizontally

\newline

[D]shrinks it vertically

Posted 1 month ago

Question

g(x)

g(x)

is the translation

9

f(x) = 10x + 8

\newline

\newline

g(x) = 10x - 82

\newline

g(x) = 10x + 98

\newline

g(x) = 10x - 1

\newline

g(x) = 10x + 17

Posted 2 months ago

Question

What kind of transformation converts the graph of

f(x) = -3x^2 - 4

into the graph of

g(x) = -3x^2 + 6

\newline

\newline

\text{[A]translation 10 units up}

\newline

\text{[B]translation 10 units down}

\newline

\text{[C]translation 10 units left}

\newline

\text{[D]translation 10 units right}

Posted 1 month ago

Question

y=x^{2}

is scaled vertically by a factor of

7

. What is the equation of the new parabola?

\newline

y=

Posted 4 months ago

Question

y=x^{2}

is shifted down by

6

units and to the right by

5

\newline

What is the equation of the new parabola?

\newline

y=

Posted 4 months ago

Question

y=x^{2}

is shifted up by

2

units and to the right by

3

\newline

What is the equation of the new parabola?

\newline

y=

Posted 1 month ago

Question

y=x^{2}

is reflected across the

x

-axis and then scaled vertically by a factor of

5

\newline

What is the equation of the new parabola?

\newline

y=\square

Posted 2 months ago

Question

y=x^{2}

is scaled vertically by a factor of

\frac{1}{10}

\newline

What is the equation of the new parabola?

\newline

y=

Posted 3 months ago