AI tutor
Full solution
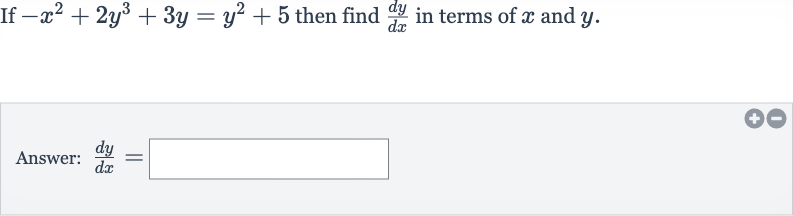
Q. If then find in terms of and .Answer:
- Rewrite Equation: First, we need to rewrite the given equation to make it easier to differentiate with respect to . The equation is .
- Differentiate with Respect to : Now, we will differentiate both sides of the equation with respect to . Remember that when differentiating terms with , we treat as a function of and use the chain rule to include .
- Left Side Differentiation: Differentiate the left side of the equation with respect to : . This gives us .
- Right Side Differentiation: Differentiate the right side of the equation with respect to : . This gives us , since the derivative of a constant is .
- Solve for (\frac{dy}{dx}): Now we have the following equation from the derivatives: \(\(-2x + y^{} \cdot (\frac{dy}{dx}) + \cdot (\frac{dy}{dx}) = y \cdot (\frac{dy}{dx}).
- Collect Terms: We need to solve for . To do this, we'll collect all the terms with on one side of the equation and the rest on the other side. This gives us .
- Factor Out from the left side of the equation: .
- Isolate by dividing both sides of the equation by .