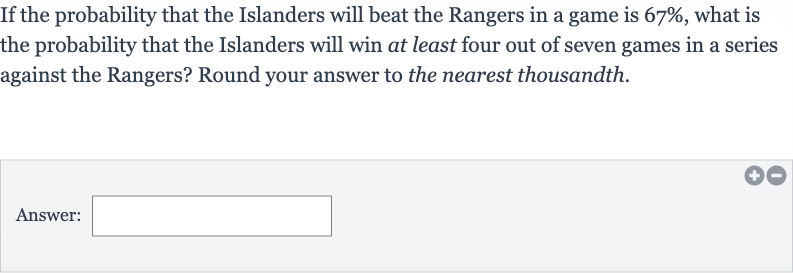
If the probability that the Islanders will beat the Rangers in a game is 67%, what is the probability that the Islanders will win at least four out of seven games in a series against the Rangers? Round your answer to the nearest thousandth. Answer:

Question

If the probability that the Islanders will beat the Rangers in a game is  67%, what is the probability that the Islanders will win at least four out of seven games in a series against the Rangers? Round your answer to the nearest thousandth. Answer:

Bytelearn · Accepted Answer

Understand the problem: Understand the problem and determine the approach. We need to calculate the probability of the Islanders winning at least 4 out of 7 games. This is a binomial probability problem because each game has two outcomes (win or lose), and we want to find the probability of a certain number of wins in a fixed number of trials (games).Calculate wins probability: Calculate the probability of winning exactly 4, 5, 6, and 7 games. We will use the binomial probability formula: P(X = k) = C(n, k) * p^k * (1-p)^(n-k), where: - P(X = k) is the probability of k wins, - C(n, k) is the combination of n games taken k at a time, - p is the probability of winning one game (67% or 0.67), - n is the total number of games (7), - k is the number of games won (which we will calculate for 4, 5, 6, and 7).Calculate 4 games probability: Calculate the probability of winning exactly 4 games. Using the binomial formula, we find P(X = 4): C(7, 4) * 0.67^4 * (1-0.67)^(7-4) = 35 * 0.67^4 * 0.33^3 = 35 * 0.20151121 * 0.035937 = 35 * 0.007237 ≈ 0.2533Calculate 5 games probability: Calculate the probability of winning exactly 5 games. Using the binomial formula, we find P(X = 5): C(7, 5) * 0.67^5 * (1-0.67)^(7-5) = 21 * 0.67^5 * 0.33^2 = 21 * 0.13207934 * 0.1089 = 21 * 0.014379 ≈ 0.3019Calculate 6 games probability: Calculate the probability of winning exactly 6 games. Using the binomial formula, we find P(X = 6): C(7, 6) * 0.67^6 * (1-0.67)^(7-6) = 7 * 0.67^6 * 0.33^1 = 7 * 0.08803834 * 0.33 = 7 * 0.029046 ≈ 0.2033Calculate 7 games probability: Calculate the probability of winning all 7 games. Using the binomial formula, we find P(X = 7): C(7, 7) * 0.67^7 * (1-0.67)^(7-7) = 1 * 0.67^7 * 0.33^0 = 1 * 0.06706822 * 1 = 0.06706822 ≈ 0.0671Calculate total probability: Add the probabilities of winning exactly 4, 5, 6, and 7 games to find the total probability of winning at least 4 games. Total probability = P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) ≈ 0.2533 + 0.3019 + 0.2033 + 0.0671 ≈ 0.8256Round total probability: Round the total probability to the nearest thousandth. Rounded probability = 0.826

If the probability that the Islanders will beat the Rangers in a game is $67 \%$ , what is the probability that the Islanders will win at least four out of seven games in a series against the Rangers? Round your answer to the nearest thousandth. $\newline$ Answer:

Full solution

More problems from Find probabilities using the binomial distribution

Related topics

If the probability that the Islanders will beat the Rangers in a game is 67% 67 \% 67%, what is the probability that the Islanders will win at least four out of seven games in a series against the Rangers? Round your answer to the nearest thousandth.\newlineAnswer:

If the probability that the Islanders will beat the Rangers in a game is $67 \%$ , what is the probability that the Islanders will win at least four out of seven games in a series against the Rangers? Round your answer to the nearest thousandth. $\newline$ Answer: