Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

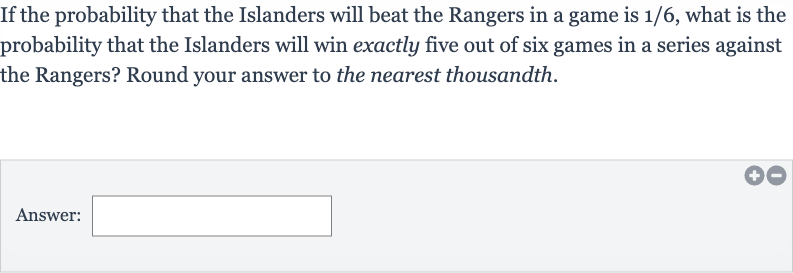
If the probability that the Islanders will beat the Rangers in a game is 1//6, what is the probability that the Islanders will win exactly five out of six games in a series against the Rangers? Round your answer to the nearest thousandth. Answer:

If the probability that the Islanders will beat the Rangers in a game is 1/6 1 / 6 , what is the probability that the Islanders will win exactly five out of six games in a series against the Rangers? Round your answer to the nearest thousandth.\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find probabilities using the binomial distributionright chevron icon

Full solution

Q. If the probability that the Islanders will beat the Rangers in a game is 1/6 1 / 6 , what is the probability that the Islanders will win exactly five out of six games in a series against the Rangers? Round your answer to the nearest thousandth.\newlineAnswer:
  1. Understand Problem and Formula: Understand the problem and determine the formula to use.\newlineWe need to calculate the probability of the Islanders winning exactly five out of six games. This is a binomial probability problem, where the number of trials is 66, the number of successes is 55, and the probability of success on a single trial is 16\frac{1}{6}. The formula for the probability of exactly kk successes in nn trials is:\newlineP(X=k)=(nk)⋅(pk)⋅((1−p)(n−k))P(X = k) = \binom{n}{k} \cdot (p^k) \cdot ((1-p)^{(n-k)})\newlinewhere (nk)\binom{n}{k} is the binomial coefficient, pp is the probability of success, and (1−p)(1-p) is the probability of failure.
  2. Calculate Binomial Coefficient: Calculate the binomial coefficient for 55 successes in 66 trials.\newlineThe binomial coefficient (nn choose kk) is calculated as:\newline(n(n choose kk) = n!k!⋅(n−k)!\frac{n!}{k! \cdot (n-k)!}\newlineFor our problem, this is:\newline(6(6 choose 55) = 6!5!⋅(6−5)!\frac{6!}{5! \cdot (6-5)!}\newline= 6600\newline= 66
  3. Calculate Probability of 55 Successes: Calculate the probability of exactly 55 successes (wins) and 11 failure (loss).\newlineUsing the formula from Step 11, we have:\newlineP(X=5)=(65)⋅(16)5⋅(56)1P(X = 5) = \binom{6}{5} \cdot \left(\frac{1}{6}\right)^5 \cdot \left(\frac{5}{6}\right)^1\newlineNow we plug in the values from Step 22:\newlineP(X=5)=6⋅(16)5⋅(56)1P(X = 5) = 6 \cdot \left(\frac{1}{6}\right)^5 \cdot \left(\frac{5}{6}\right)^1
  4. Perform Calculations: Perform the calculations.\newlineP(X=5)=6×(16)5×(56)P(X = 5) = 6 \times \left(\frac{1}{6}\right)^5 \times \left(\frac{5}{6}\right)\newline=6×(17776)×(56)= 6 \times \left(\frac{1}{7776}\right) \times \left(\frac{5}{6}\right)\newline=6×57776= 6 \times \frac{5}{7776}\newline=307776= \frac{30}{7776}\newline=1259= \frac{1}{259}
  5. Convert Probability to Decimal: Convert the probability to a decimal and round to the nearest thousandth.\newline1259\frac{1}{259} is approximately equal to 0.003860.00386 when converted to a decimal.\newlineRounded to the nearest thousandth, this is 0.0040.004.

More problems from Find probabilities using the binomial distribution

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 9 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 9 months ago

Question
Y Y is the number of desserts available in a randomly chosen restaurant.\newlineIs the random variable Y Y discrete or continuous?\newlineChoices:\newline[A]discrete \text{[A]discrete} \newline[B]continuous \text{[B]continuous}
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous for all real numbers?\newlineg(x)=ln⁡(x) g(x)=\ln (x) \newlinef(x)=1x f(x)=\frac{1}{x} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newlineD Neither g g nor f f
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous at x=−1 x=-1 ?\newlineg(x)=sin⁡(x+1) g(x)=\sin (x+1) \newlinef(x)=1x−1 f(x)=\frac{1}{x-1} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newline(D) Neither g g nor f f
Get tutor helpright-arrow

Posted 8 months ago

Question
Let g g be a continuous function on the closed interval [−1,4] [-1,4] , where g(−1)=−4 g(-1)=-4 and g(4)=1 g(4)=1 .\newlineWhich of the following is guaranteed by the Intermediate Value Theorem?\newlineChoose 11 answer:\newline(A) g(c)=−3 g(c)=-3 for at least one c c between −1-1 and 44\newline(B) g(c)=3 g(c)=3 for at least one c c between −4-4 and 11\newline(C) g(c)=−3 g(c)=-3 for at least one c c between −4-4 and 11\newline(D) g(c)=3 g(c)=3 for at least one c c between −1-1 and 44
Get tutor helpright-arrow

Posted 8 months ago

View all (89)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant