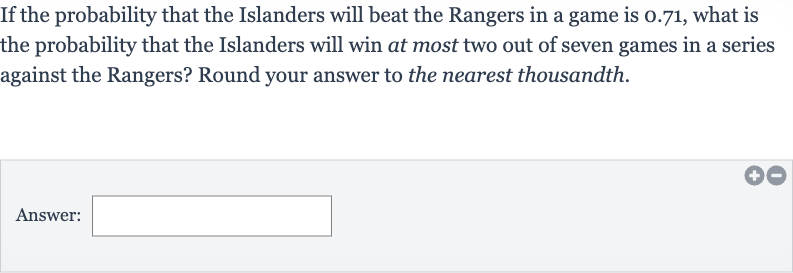
If the probability that the Islanders will beat the Rangers in a game is $0$ . $71$ , what is the probability that the Islanders will win at most two out of seven games in a series against the Rangers? Round your answer to the nearest thousandth. $\newline$ Answer:

View step-by-step help

Home

Math Problems

Algebra 2

Find probabilities using the binomial distribution

Full solution

Q. If the probability that the Islanders will beat the Rangers in a game is

0

71

, what is the probability that the Islanders will win at most two out of seven games in a series against the Rangers? Round your answer to the nearest thousandth.

\newline

Answer:

Identify Formula and Values: Identify the binomial probability formula and the values of $n$ , $k$ , and $p$ . The binomial probability formula is $P(X = k) = C(n, k) \cdot (p)^k \cdot (1-p)^{(n-k)}$ , where $n$ is the number of trials, $k$ is the number of successes, and $p$ is the probability of success on a single trial. For this problem, $n = 7$ (seven games in a series), $p = 0.71$ (probability that the Islanders will beat the Rangers in a game), and $k$ will take on the values $k$ $0$ , $k$ $1$ , and $k$ $2$ because we are looking for the probability of the Islanders winning at most two games.
Calculate Probability for $k = 0$ : Calculate the probability for $k = 0$ . Using the binomial probability formula, we calculate $P(X = 0)$ : $P(X = 0) = C(7, 0) \times (0.71)^0 \times (1-0.71)^{7-0}$ $C(7, 0)$ is the number of ways to choose $0$ games out of $7$ , which is $1$ . $(0.71)^0$ is $1$ because any number to the power of $0$ is $1$ . $k = 0$ $2$ is $k = 0$ $3$ . Now we calculate $k = 0$ $3$ .
Calculate $(0.29)^7$ : Calculate $(0.29)^7$ .
$(0.29)^7 = 0.29 \times 0.29 \times 0.29 \times 0.29 \times 0.29 \times 0.29 \times 0.29$
This calculation gives us approximately $0.0005741$ .
Now we can calculate $P(X = 0)$ :
$P(X = 0) = 1 \times 1 \times 0.0005741 = 0.0005741$ .
Calculate Probability for $k = 1$ : Calculate the probability for $k = 1$ . Using the binomial probability formula, we calculate $P(X = 1)$ : $P(X = 1) = C(7, 1) \cdot (0.71)^1 \cdot (1-0.71)^{(7-1)}$ $C(7, 1)$ is the number of ways to choose $1$ game out of $7$ , which is $7$ . $(0.71)^1$ is $0.71$ . $(1-0.71)^{(7-1)}$ is $(0.29)^6$ . Now we calculate $(0.29)^6$ .
Calculate $(0.29)^6$ : Calculate $(0.29)^6$ .
$(0.29)^6 = 0.29 \times 0.29 \times 0.29 \times 0.29 \times 0.29 \times 0.29$
This calculation gives us approximately $0.001979$ .
Now we can calculate $P(X = 1)$ :
$P(X = 1) = 7 \times 0.71 \times 0.001979 = 0.00994049$ .
Calculate Probability for $k = 2$ : Calculate the probability for $k = 2$ . Using the binomial probability formula, we calculate $P(X = 2)$ : $P(X = 2) = C(7, 2) \cdot (0.71)^2 \cdot (1-0.71)^{(7-2)}$ $C(7, 2)$ is the number of ways to choose $2$ games out of $7$ , which is $\frac{7!}{2! \cdot (7-2)!} = 21$ . $(0.71)^2$ is approximately $0.5041$ . $(1-0.71)^{(7-2)}$ is $(0.29)^5$ . Now we calculate $(0.29)^5$ .
Calculate $(0.29)^5$ : Calculate $(0.29)^5$ .
$(0.29)^5 = 0.29 \times 0.29 \times 0.29 \times 0.29 \times 0.29$
This calculation gives us approximately $0.006408$ .
Now we can calculate $P(X = 2)$ :
$P(X = 2) = 21 \times 0.5041 \times 0.006408 = 0.0679057688$ .
Calculate Total Probability: Calculate the total probability for $k = 0$ , $k = 1$ , and $k = 2$ . The total probability that the Islanders will win at most two out of seven games is the sum of the probabilities for $k = 0$ , $k = 1$ , and $k = 2$ : $P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)$ $P(X \leq 2) = 0.0005741 + 0.00994049 + 0.0679057688$ $P(X \leq 2) = 0.0784203588$ Round this to the nearest thousandth to get the final answer.