Full solution
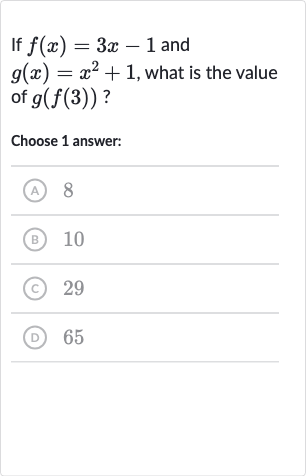
Q. If and , what is the value of ?Choose answer:(A) (B) (C) (D)
- Find : First, we need to find the value of by substituting with in the function .
- Calculate : Now that we have , we need to find the value of by substituting into the function .
More problems from Evaluate expression when a complex numbers and a variable term is given
QuestionGet tutor help
QuestionGet tutor help