Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If
f(x)=2^(2x)+10, what is the value of
f(-3), to the nearest ten-thousandth (if necessary)?
Answer:

If $f(x)=2^{2 x}+10$ , what is the value of $f(-3)$ , to the nearest ten-thousandth (if necessary)? $\newline$ Answer:

View step-by-step help

View step-by-step help

Solve exponential equations using logarithms

Full solution

Q. If

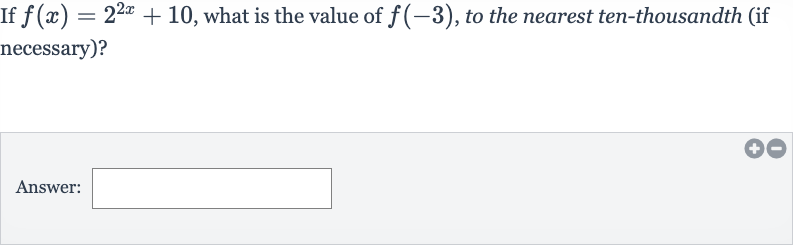
f(x)=2^{2 x}+10

, what is the value of

f(-3)

, to the nearest ten-thousandth (if necessary)?

\newline

Answer:

Substitute $x$ with $-3$ : To find the value of $f(-3)$ , we need to substitute $x$ with $-3$ in the function $f(x) = 2^{(2x)} + 10$ . $\newline$ $f(-3) = 2^{(2*(-3))} + 10$
Calculate exponent part: Now we calculate the exponent part: $2\cdot(-3) = -6$ . So we have: $\newline$ $f(-3) = 2^{-6} + 10$
Calculate $2^{-6}$ : Next, we calculate $2^{-6}$ . Since $2^{-6}$ is the same as $1/(2^6)$ , we find: $\newline$ $2^{-6} = 1/(2^6) = 1/64$
Add $10$ : Now we add $10$ to the result of $2^{-6}$ : $\newline$ $f(-3) = \frac{1}{64} + 10$
Express $10$ as fraction: To add $\frac{1}{64}$ to $10$ , we need to express $10$ as a fraction with the same denominator as $\frac{1}{64}$ : $10 = 10 \times \left(\frac{64}{64}\right) = \frac{640}{64}$
Add two fractions: Now we add the two fractions: $f(-3) = \frac{1}{64} + \frac{640}{64} = \frac{(1 + 640)}{64}$
Perform addition in numerator: We perform the addition in the numerator: $f(-3) = (1 + 640)/64 = 641/64$
Divide $641$ by $64$ : Finally, we divide $641$ by $64$ to get the decimal value: $\newline$ $f(-3) = \frac{641}{64} \approx 10.015625$

More problems from Solve exponential equations using logarithms

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago