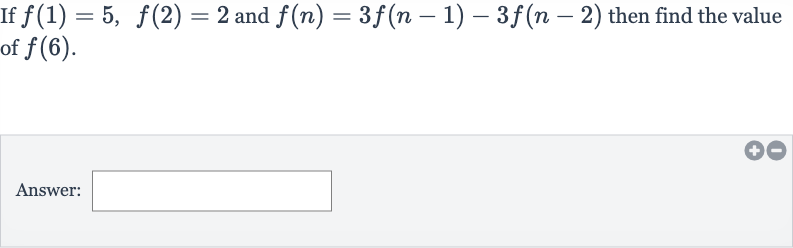AI tutor
Full solution
Q. If and then find the value of .Answer:
- Calculate : To find , we need to use the recursive formula to calculate the values of , , and first.
- Calculate : Let's calculate using the given formula: which simplifies to .
- Calculate : Substitute the known values of and into the formula: which simplifies to .
- Calculate : Calculate the value of : .
- Calculate : Calculate the value of : .Now, let's calculate using the formula: which simplifies to .
- Calculate : Calculate the value of : .Now, let's calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .
- Calculate : Calculate the value of : .Now, let's calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .
- Calculate : Calculate the value of : .Now, let's calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .Next, calculate using the formula: which simplifies to .
- Calculate : Calculate the value of : .Now, let's calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .Next, calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .
- Calculate : Calculate the value of : .Now, let's calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .Next, calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .
- Calculate : Calculate the value of : .Now, let's calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .Next, calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .Finally, calculate using the formula: which simplifies to .
- Calculate : Calculate the value of : .Now, let's calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .Next, calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .Calculate the value of : .Finally, calculate using the formula: which simplifies to .Substitute the known values of and into the formula: which simplifies to .
- Calculate f(): Calculate the value of f(): .Now, let's calculate f() using the formula: which simplifies to .Substitute the known values of f() and f() into the formula: which simplifies to .Calculate the value of f(): .Next, calculate f() using the formula: which simplifies to .Substitute the known values of f() and f() into the formula: which simplifies to .Calculate the value of f(): .Finally, calculate f() using the formula: which simplifies to .Substitute the known values of f() and f() into the formula: which simplifies to .Calculate the value of f(): .