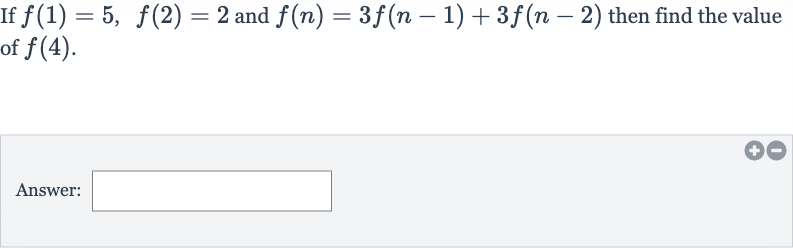Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If
f(1)=5,f(2)=2 and
f(n)=3f(n-1)+3f(n-2) then find the value of
f(4).
Answer:

If $f(1)=5, f(2)=2$ and $f(n)=3 f(n-1)+3 f(n-2)$ then find the value of $f(4)$ . $\newline$ Answer:

View step-by-step help

View step-by-step help

Find the roots of factored polynomials

Full solution

Q. If

f(1)=5, f(2)=2

and

f(n)=3 f(n-1)+3 f(n-2)

then find the value of

f(4)

.

\newline

Answer:

Given Recursive Formula: We are given the recursive formula $f(n) = 3f(n-1) + 3f(n-2)$ , and the initial conditions $f(1) = 5$ and $f(2) = 2$ . To find $f(4)$ , we first need to find $f(3)$ using the recursive formula.
Calculate $f(3)$ : Using the recursive formula, we calculate $f(3)$ as follows: $\newline$ $f(3) = 3f(2) + 3f(1)$ $\newline$ $f(3) = 3(2) + 3(5)$ $\newline$ $f(3) = 6 + 15$ $\newline$ $f(3) = 21$ $\newline$ Now we have the value of $f(3)$ .
Find $f(4)$ : Next, we use the values of $f(2)$ and $f(3)$ to find $f(4)$ using the same recursive formula: $\newline$ $f(4) = 3f(3) + 3f(2)$ $\newline$ $f(4) = 3(21) + 3(2)$ $\newline$ $f(4) = 63 + 6$ $\newline$ $f(4) = 69$ $\newline$ We have now found the value of $f(4)$ .

More problems from Find the roots of factored polynomials

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 3 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 3 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 3 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 3 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 3 months ago