AI tutor
Full solution
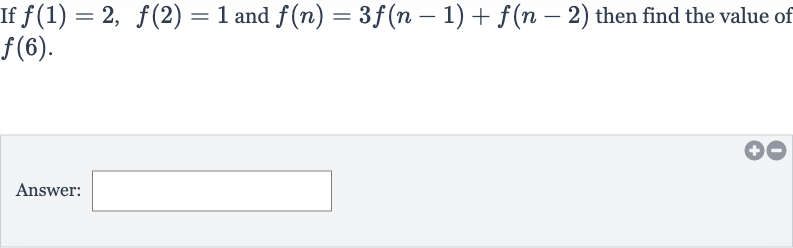
Q. If and then find the value of .Answer:
- Initialize Recursive Formula: To find the value of , we need to use the recursive formula and the initial conditions and . We will calculate the values of , , , and then step by step.
- Calculate : First, we find using the recursive formula:So,
- Calculate : Next, we find using the recursive formula:So,
- Calculate : Then, we find using the recursive formula:So,
- Calculate : Finally, we find using the recursive formula:So,