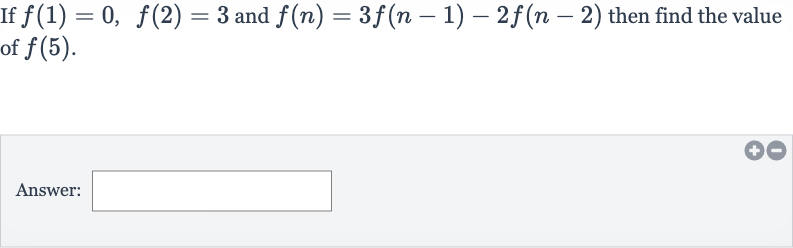AI tutor
Full solution
Q. If and then find the value of .Answer:
- Calculate : To find , we need to use the recursive formula to find the values of and first, since we already know and .
- Calculate : Let's calculate using the given formula: which simplifies to .
- Calculate : Substitute the known values and into the formula to get which simplifies to .
- Calculate : Substitute the known values and into the formula to get which simplifies to .Now let's calculate using the formula: which simplifies to .
- Calculate : Substitute the known values and into the formula to get which simplifies to .Now let's calculate using the formula: which simplifies to .Substitute the known values and into the formula to get which simplifies to , so .
- Calculate : Substitute the known values and into the formula to get which simplifies to .Now let's calculate using the formula: which simplifies to .Substitute the known values and into the formula to get which simplifies to , so .Finally, we calculate using the formula: which simplifies to .
- Calculate : Substitute the known values and into the formula to get which simplifies to .Now let's calculate using the formula: which simplifies to .Substitute the known values and into the formula to get which simplifies to , so .Finally, we calculate using the formula: which simplifies to .Substitute the known values and into the formula to get which simplifies to , so .